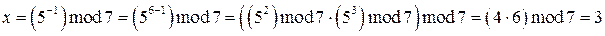 .
.
3. С помощью алгоритма Евклида.
Алгоритм Евклида применяется для нахождения НОД чисел 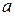 и
и 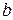 . Однако его расширенный вариант можно использовать и для вычисления обратной величины.
. Однако его расширенный вариант можно использовать и для вычисления обратной величины.
Основной вариант.
Даны 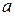 и
и 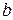 ,
, 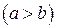 . Алгоритм имеет итерационный характер:
. Алгоритм имеет итерационный характер:
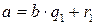 ,
, 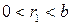 ;
;
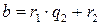 ,
, 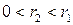 ;
;
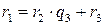 ,
, 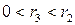 ;
;
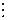
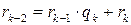 ,
, 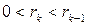 ;
;
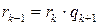 ,
, 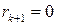 ;
;
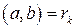 ,
,
где 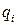 ,
, 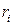 ‑ частное и остаток на
‑ частное и остаток на 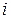 ‑м шаге алгоритма. На первом шаге делимое ‑
‑м шаге алгоритма. На первом шаге делимое ‑ 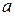 , делитель ‑
, делитель ‑ 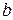 , частное ‑
, частное ‑ 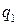 , остаток ‑
, остаток ‑ 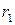 . На
. На 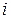 ‑м,
‑м, 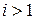 шаге алгоритма: делимое ‑ делитель
шаге алгоритма: делимое ‑ делитель 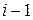 ‑го шага, делитель ‑ остаток
‑го шага, делитель ‑ остаток 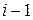 ‑го шага (
‑го шага (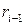 ), частное ‑
), частное ‑ 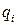 , остаток ‑
, остаток ‑ 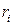 .
.
Пример 6.3. Пусть 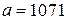 и
и 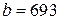 . Найти
. Найти 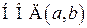 .
.
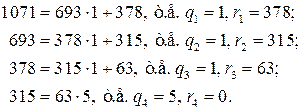
То есть на четвертом шаге остаток от деления 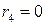 , следовательно, алгоритм останавливается и
, следовательно, алгоритм останавливается и 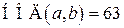 .
.
Доказано, что при неотрицательных 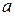 и
и 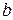 можно найти такие целые числа:
можно найти такие целые числа: 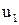 ,
, 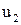 ,
, 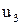 , что будет выполняться
, что будет выполняться
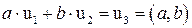 .
.
Если выбрать 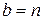 и
и 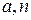 ‑ взаимно простые числа, т.е.
‑ взаимно простые числа, т.е. 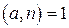 , тогда
, тогда
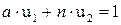 ,
,
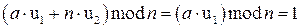 ,
,
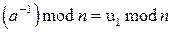 .
.
То есть для нахождения обратной величины необходимо вычислить 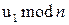 . Эта задача решается в ходе вычисления
. Эта задача решается в ходе вычисления 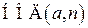 в соответствии с алгоритмом Евклида. Дополнительно на каждом шаге вычисляются координаты двух векторов:
в соответствии с алгоритмом Евклида. Дополнительно на каждом шаге вычисляются координаты двух векторов:
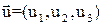 ,
, 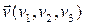 .
.
Алгоритм вычисления 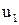 имеет следующий вид
имеет следующий вид
1. Начальные установки:
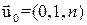 , т.е.
, т.е. 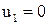 ,
, 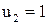 ,
, 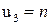 . При этом
. При этом 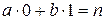 , т.е.
, т.е. 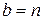 ,
,
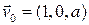 , т.е.
, т.е. 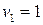 ,
, 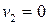 ,
, 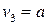 . При этом
. При этом 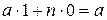 .
.
2. Проверяем, выполняется ли 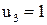 , если да, то алгоритм заканчивается.
, если да, то алгоритм заканчивается.
3. Делим 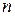 на
на 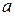 (
(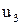 на
на 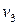 ) и определяем:
) и определяем:
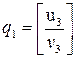 и значения векторов:
и значения векторов: 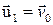 ;
; 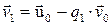 .
.
4. Вернуться к шагу 2.
На каждом шаге при расчетах используются результаты предыдущего:
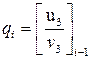 ,
, 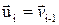 ,
, 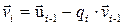 .
.
При 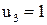 вычисления заканчиваются
вычисления заканчиваются 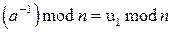 , где
, где 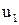 значение
значение 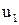 , полученное на последнем шаге.
, полученное на последнем шаге.
Пример 6.4. Пусть 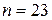 и
и 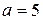 . Найти число
. Найти число 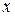 , обратное числу
, обратное числу 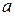 по модулю
по модулю 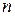 , т.е. найти
, т.е. найти 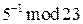 .
.
Используя расширенный алгоритм Евклида, выполним вычисления.
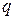
| 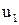
| 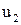
| 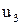
| 
| 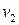
| 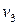
|
| - | 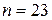
| 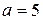
| ||||
| -4 | ||||||
| -4 | -1 | |||||
| -1 | -9 | |||||
| - | -9 |
При 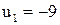 ,
, 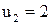 ,
, 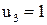 выполняется уравнение
выполняется уравнение 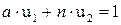 ,
, 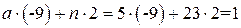 и
и 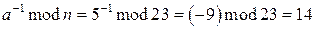 .
.
Итак, 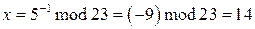 .
.
 2015-04-01
2015-04-01 545
545








