Название «симплекс-метод» связано с тем, что он впервые разрабатывался применительно к задачам линейного программирования, в которых допустимое множество представляло собой симплекс:
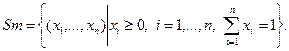
Другое название симплекс-метода – метод последовательного улучшения плана.
Рассмотрим каноническую задачу линейного программирования:
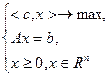 (2.2.1)
(2.2.1)
Допустимое множество задачи (2.2.1) может быть задано выражением:
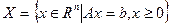 . (2.2.2)
. (2.2.2)
Столбцы матрицы 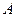 размерности
размерности 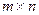 образуют
образуют 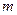 -мерные векторы
-мерные векторы
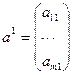 ,…,
,…, 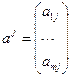 ,…,
,…, 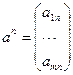 ;
; 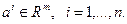 (2.2.3)
(2.2.3)
Условие 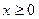 в (2.2.1),
в (2.2.1), 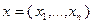 , означает, что
, означает, что 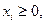
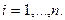 Рас-
Рас-
смотрим множество
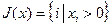 , (2.2.4)
, (2.2.4)
т.е. множество, состоящее из индексов при положительных координатах вектора 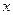 . Тогда
. Тогда
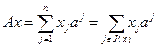 .
.
Напомним, что 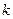 векторов
векторов 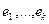 линейно независимы, если из
линейно независимы, если из 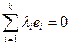 следует
следует 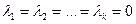 . Теперь введем понятие опорной точки.
. Теперь введем понятие опорной точки.
Точка 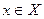 называется опорной точкой в задаче (2.2.1), если векторы
называется опорной точкой в задаче (2.2.1), если векторы 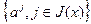 линейно независимы.
линейно независимы.
Справедливы следующие утверждения:
1) если в задаче (2.2.1) множество 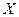 не пусто, то оно имеет опорные точки и число их конечно;
не пусто, то оно имеет опорные точки и число их конечно;
2) если множество решений задачи (2.2.1) не пусто, то оно содержит хотя бы одну опорную точку из множества 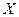 .
.
Пример 2.2.1. Найти опорные точки и решение задачи:
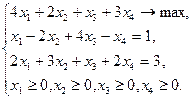
Здесь 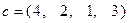 ,
, 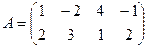 ,
, 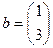 ,
, 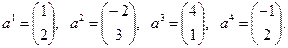
Линейно независимым совокупностям столбцов матрицы 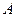 соответствуют следующие наборы индексов
соответствуют следующие наборы индексов 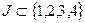 :
: 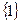 ,
, 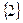 ,
, 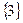 ,
, 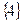 ,
, 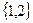 ,
, 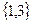 ,
, 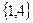 ,
, 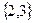 ,
, 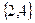 ,
, 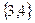 . Для каждого из этих наборов будем решать систему уравнений
. Для каждого из этих наборов будем решать систему уравнений
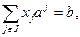 (2.2.5)
(2.2.5)
которая может иметь либо единственное решение, либо не иметь решений. Если решение есть, то необходимо проверить, все ли 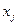 в решении положительны. Если все
в решении положительны. Если все 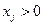 , то они участвуют в формировании опорной точки, остальные координаты которой равны нулю. Если система (2.2.5) не имеет решений или не все
, то они участвуют в формировании опорной точки, остальные координаты которой равны нулю. Если система (2.2.5) не имеет решений или не все 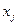 в решении положительны, то опорную точку для рассматриваемого набора индексов сформировать невозможно.
в решении положительны, то опорную точку для рассматриваемого набора индексов сформировать невозможно.
Рассмотрим набор 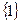 . В этом случае система (2.2.5) имеет вид:
. В этом случае система (2.2.5) имеет вид:
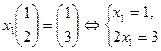 – решений нет.
– решений нет.
Такой же результат дает рассмотрение наборов 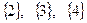 . Это означает, что ни один из столбцов матрицы
. Это означает, что ни один из столбцов матрицы 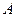 не коллинеарен вектору
не коллинеарен вектору 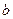 . Рассмотрим набор
. Рассмотрим набор 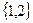 . В этом случае система (2.2.5) может быть записана в виде:
. В этом случае система (2.2.5) может быть записана в виде:
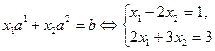 и имеет решение
и имеет решение 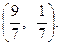
Оба значения в решении положительны. Формируем опорную точку: 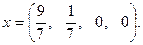 Находим значение целевой функции в опорной точке:
Находим значение целевой функции в опорной точке: 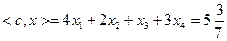 . Набору
. Набору 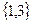 соответствует система
соответствует система
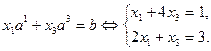
Ее решение 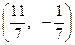 содержит отрицательное значение, поэтому опорную точку в данном случае сформировать невозможно. Перейдем к рассмотрению набора
содержит отрицательное значение, поэтому опорную точку в данном случае сформировать невозможно. Перейдем к рассмотрению набора 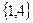 . Система уравнений типа (2.2.5) в этом случае имеет вид:
. Система уравнений типа (2.2.5) в этом случае имеет вид:
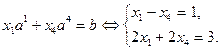
Ее решение 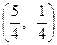 позволяет сформировать опорную точку
позволяет сформировать опорную точку 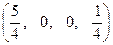 , в которой
, в которой 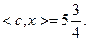 Действуя аналогичным образом, для оставшихся наборов получаем следующие результаты:
Действуя аналогичным образом, для оставшихся наборов получаем следующие результаты:
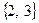 – дает опорную точку
– дает опорную точку 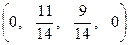 , в которой
, в которой 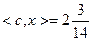 ;
;
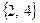 – не позволяет сформировать опорную точку, так как решение системы уравнений
– не позволяет сформировать опорную точку, так как решение системы уравнений 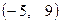 содержит отрицательное значение;
содержит отрицательное значение;
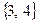 – дает опорную точку
– дает опорную точку 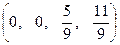 , в которой
, в которой 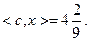
Максимальное из найденных значений целевой функции 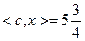 получено в опорной точке
получено в опорной точке 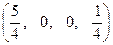 , которая и является решением задачи.
, которая и является решением задачи.
Следует отметить, что метод перебора, использованный в рассмотренном примере, на практике неприменим из-за недопустимо больших затрат времени на полный перебор в реальных задачах. Это подтверждает следующий оценочный расчет.
Пусть любые 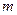 векторов из
векторов из 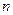 векторов (2.2.3) линейно независимы. Тогда число случаев, которые необходимо рассмотреть при фиксированном
векторов (2.2.3) линейно независимы. Тогда число случаев, которые необходимо рассмотреть при фиксированном 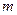 , составит
, составит
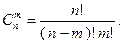 (2.2.6)
(2.2.6)
В рассмотренном выше примере 2.2.1 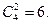 Для вычисления факториала
Для вычисления факториала 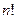 при больших значениях
при больших значениях 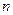 можно воспользоваться приближенным выражением, полученным из формулы Стирлинга:
можно воспользоваться приближенным выражением, полученным из формулы Стирлинга:
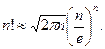
Тогда, считая значения 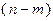 и
и 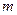 также большими, из (2.2.6) получим:
также большими, из (2.2.6) получим:
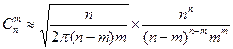 .
.
Например, при 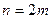 получим
получим
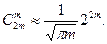
Для решения системы 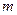 линейных уравнений требуется выполнить приблизительно
линейных уравнений требуется выполнить приблизительно 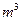 простейших арифметических операций. Тогда суммарное число операций для решения
простейших арифметических операций. Тогда суммарное число операций для решения 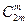 систем уравнений составит
систем уравнений составит
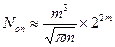 .
.
Операции, необходимые для проверки решений систем на положительность, учитывать не будем. При 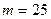 ,
, 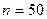 из последнего выражения получаем
из последнего выражения получаем 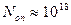 . Пусть быстродействие вычислителя составляет
. Пусть быстродействие вычислителя составляет 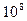 операций в секунду. Тогда приближенное значение времени, требуемого на вычисления, составит
операций в секунду. Тогда приближенное значение времени, требуемого на вычисления, составит 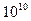 с или примерно 300 лет.
с или примерно 300 лет.
В симплекс-методе предусмотрен направленный перебор опорных точек, при котором значение целевой функции в каждой очередной опорной точке строго больше, чем в предыдущей. Общее количество таких шагов при решении практических задач обычно составляет от 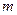 до
до 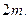
Опорная точка 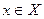 (см. (2.2.2)) называется невырожденной, если
(см. (2.2.2)) называется невырожденной, если
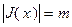 (2.2.7)
(2.2.7)
(мощность множества 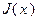 равна
равна 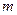 ). Если в задаче линейного программирования (2.2.1) все опорные точки невырождены, то задача называется невырожденной. Симплекс-метод будем рассматривать применительно к невырожденным задачам. Вырожденная задача может быть сведена к невырожденной путем алгебраических преобразований.
). Если в задаче линейного программирования (2.2.1) все опорные точки невырождены, то задача называется невырожденной. Симплекс-метод будем рассматривать применительно к невырожденным задачам. Вырожденная задача может быть сведена к невырожденной путем алгебраических преобразований.
Пусть 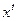 – очередная опорная точка, рассчитываемая в соответствии с алгоритмом работы симплекс-метода. Возможен один из трех вариантов:
– очередная опорная точка, рассчитываемая в соответствии с алгоритмом работы симплекс-метода. Возможен один из трех вариантов:
1) 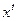 является решением задачи (2.2.1);
является решением задачи (2.2.1);
2) задача (2.2.1) не имеет решений;
3) рассчитывается следующая опорная точка 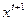 , причем
, причем
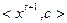 >
> 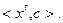
Вопрос об отыскании начальной опорной точки 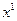 будет рассмотрен позже. Будем полагать, что получено значение
будет рассмотрен позже. Будем полагать, что получено значение 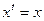 и раскроем условия реализации и содержание каждого из трех перечисленных выше вариантов.
и раскроем условия реализации и содержание каждого из трех перечисленных выше вариантов.
Поскольку 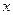 – опорная точка и задача невырождена, столбцы
– опорная точка и задача невырождена, столбцы 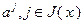 линейно независимы и выполнено (2.2.7). Столбцы
линейно независимы и выполнено (2.2.7). Столбцы 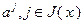 образуют базис в
образуют базис в 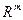 . Разложение произвольного вектора
. Разложение произвольного вектора 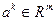 по базису
по базису 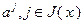 имеет вид:
имеет вид:
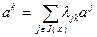 , (2.2.8)
, (2.2.8)
где 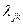 – коэффициенты разложения.
– коэффициенты разложения.
Введем в рассмотрение величину
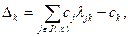
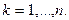 (2.2.9)
(2.2.9)
Здесь 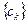 – координаты вектора
– координаты вектора 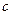 из целевой функции рассматриваемой задачи (2.2.1);
из целевой функции рассматриваемой задачи (2.2.1); 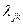 – коэффициенты из (2.2.8).
– коэффициенты из (2.2.8).
Если 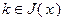 , то
, то
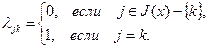 (2.2.10)
(2.2.10)
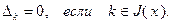 (2.2.11)
(2.2.11)
Теорема 2.2.1 (правило оптимальности).
Если 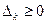
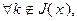 то
то 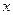 – решение задачи (2.2.1).
– решение задачи (2.2.1).
Доказательство. Используя (2.2.1), (2.2.3) и (2.2.4), запишем:
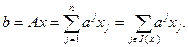 (2.2.12)
(2.2.12)
Последняя сумма в (2.2.12) не содержит нулевых слагаемых. Рассмотрим произвольную точку 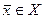 , где
, где 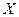 – допустимое множество задачи (2.2.1), определяемое согласно (2.2.2). Эта точка удовлетворяет уравнению
– допустимое множество задачи (2.2.1), определяемое согласно (2.2.2). Эта точка удовлетворяет уравнению
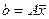 , (2.2.13)
, (2.2.13)
правую часть которого преобразуем следующим образом:
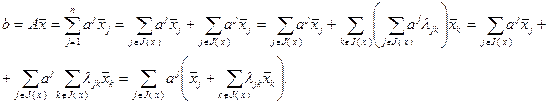
Сравнивая полученное выражение с (2.2.12) и учитывая, что точку можно разложить по базису единственным образом, приходим к выводу о справедливости равенства
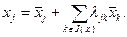 (2.2.14)
(2.2.14)
Подчеркнем, что (2.2.14) справедливо 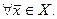 Найдем значение целевой функции в точке
Найдем значение целевой функции в точке 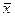 :
:
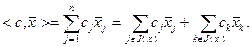 (2.2.15)
(2.2.15)
Из условия теоремы, а также из (2.2.9) и (2.2.11) следует:
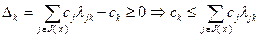
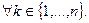
Подстановка правой части последнего неравенства в (2.2.15) вместо 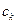 приводит к неравенству
приводит к неравенству
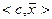
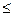
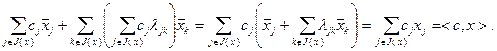
В процессе преобразований использовано выражение (2.2.14). Таким образом, 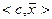
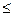
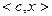 . Следовательно,
. Следовательно, 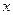 – решение задачи (2.2.1). Теорема доказана.
– решение задачи (2.2.1). Теорема доказана.
Допустим, что условие теоремы 2.2.1 не выполнено, т.е. 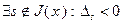 . По аналогии с (2.2.8) имеем
. По аналогии с (2.2.8) имеем
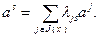 (2.2.16)
(2.2.16)
Используя (2.2.16), запишем:
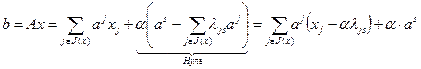 , (2.2.17)
, (2.2.17)
где 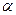 – произвольное действительное число. Введем точку
– произвольное действительное число. Введем точку 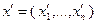 , координаты которой формируются следующим образом:
, координаты которой формируются следующим образом:
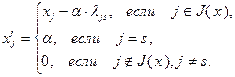 (2.2.18)
(2.2.18)
Используя (2.2.18), преобразуем выражение (2.2.17):
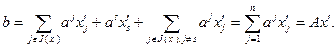 (2.2.19)
(2.2.19)
Найдем значение целевой функции в точке 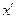 :
:
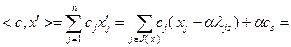
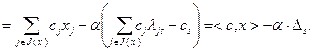 (2.2.20)
(2.2.20)
Теорема 2.2.2 (правило отсутствия решения у задачи).
Если 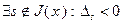 и если
и если 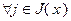
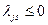 , то задача (2.2.1) не имеет решения.
, то задача (2.2.1) не имеет решения.
Доказательство. Рассмотрим вектор 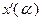 ,
, 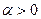 , определенный в соответствии с (2.2.18);
, определенный в соответствии с (2.2.18); 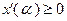 , так как
, так как 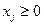
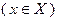 ,
, 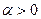 и
и 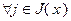
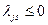 . Кроме того, согласно (2.2.19),
. Кроме того, согласно (2.2.19), 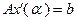 . Таким образом,
. Таким образом, 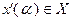 . Из (2.2.20) следует, что
. Из (2.2.20) следует, что
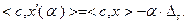 (2.2.21)
(2.2.21)
Если задать последовательность значений 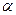 в виде
в виде 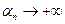 , то
, то 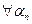
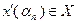 , т.е. все точки будут принадлежать допустимому множеству (2.2.2) задачи, при этом в соответствии с (2.2.21) значения целевой функции будут стремиться к бесконечности:
, т.е. все точки будут принадлежать допустимому множеству (2.2.2) задачи, при этом в соответствии с (2.2.21) значения целевой функции будут стремиться к бесконечности:
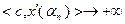 ,
,
т.е. максимум не достигается и, следовательно, задача не имеет решения. Теорема доказана.
Теорема 2.2.3.
Если 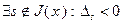 и
и 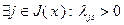 , то в невырожденной задаче (2.2.1) с помощью симплекс-метода можно осуществить переход от опорной точки, не являющейся решением задачи, к другой опорной точке со строгим увеличением значения целевой функции
, то в невырожденной задаче (2.2.1) с помощью симплекс-метода можно осуществить переход от опорной точки, не являющейся решением задачи, к другой опорной точке со строгим увеличением значения целевой функции 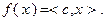
Доказательство. Введем величину 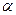 , которую определим следующим образом:
, которую определим следующим образом:
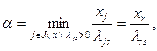
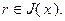 (2.2.22)
(2.2.22)
Отметим, что 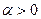 в силу (2.2.22) и (2.2.4). Подстановка
в силу (2.2.22) и (2.2.4). Подстановка 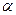 в (2.2.18)
в (2.2.18)
позволяет сформировать координаты точки 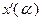 , иными словами, осуществить переход от опорной точки
, иными словами, осуществить переход от опорной точки 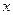 к точке
к точке 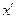 . По условию теоремы
. По условию теоремы 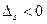 и поскольку
и поскольку 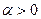 , с учетом (2.2.21) заключаем, что значение целевой функции в точке
, с учетом (2.2.21) заключаем, что значение целевой функции в точке 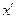 строго больше, чем в предыдущей точке
строго больше, чем в предыдущей точке 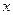 . Покажем, что точка
. Покажем, что точка 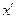 является допустимой точкой задачи (2.2.1).
является допустимой точкой задачи (2.2.1).
Очевидно, что (2.2.19) выполнено. Осталось показать, что 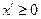 . Это следует из (2.2.18) с учетом того, что
. Это следует из (2.2.18) с учетом того, что 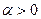 , а также
, а также
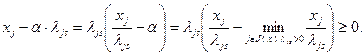
Итак, при переходе к очередной опорной точке ее координаты определяются в соответствии с (2.2.18), где в качестве величины 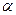 используется значение (2.2.22). В этом случае выражение (2.2.18) можно записать в более подробном виде:
используется значение (2.2.22). В этом случае выражение (2.2.18) можно записать в более подробном виде:
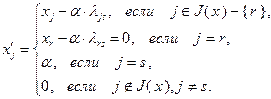 (2.2.23)
(2.2.23)
Рассмотрим множество 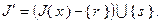 Очевидно, что
Очевидно, что 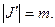 Покажем, что векторы
Покажем, что векторы 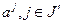 образуют базис в пространстве
образуют базис в пространстве 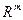 . Произвольный вектор
. Произвольный вектор 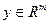 может быть представлен в виде разложения по базису
может быть представлен в виде разложения по базису 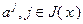 :
:
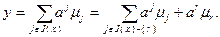 (2.2.24)
(2.2.24)
Согласно (2.2.8), 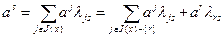 . Отсюда находим:
. Отсюда находим:
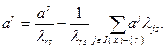 (2.2.25)
(2.2.25)
Подставив это выражение в (2.2.24), получим:
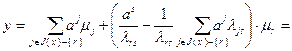
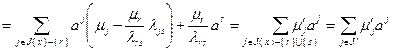 , (2.2.26)
, (2.2.26)
где 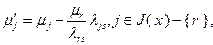
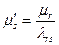 .
.
Итак, в соответствии с (2.2.26), произвольный вектор 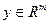 выражен через
выражен через 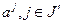 . Следовательно, множество векторов
. Следовательно, множество векторов 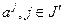 образует базис в пространстве
образует базис в пространстве 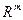 и, таким образом, векторы
и, таким образом, векторы 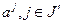 линейно независимы. Отсюда следует, что точка
линейно независимы. Отсюда следует, что точка 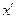 , координаты которой определяются в соответствии с (2.2.23), является опорной, причем
, координаты которой определяются в соответствии с (2.2.23), является опорной, причем 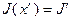 . Теорема доказана.
. Теорема доказана.
После определения новой опорной точки 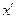 и множества
и множества 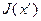 формулы (2.2.8) и (2.2.9) приобретают вид:
формулы (2.2.8) и (2.2.9) приобретают вид:
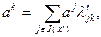
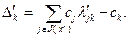 (2.2.27)
(2.2.27)
Способ вычисления коэффициентов разложения по базису 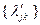 , а также значения
, а также значения 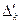 устанавливает следующая теорема.
устанавливает следующая теорема.
Теорема 2.2.4 (связь между параметрами итераций).
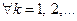 справедливы соотношения:
справедливы соотношения:
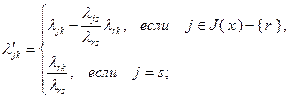 (2.2.28)
(2.2.28)
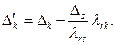 (2.2.29)
(2.2.29)
Доказательство. Используя соотношения (2.2.8) и (2.2.25), выполним следующие преобразования:
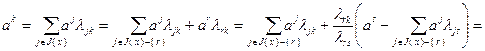
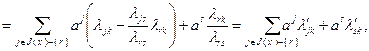 (2.2.30)
(2.2.30)
где 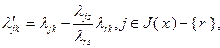
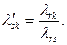
Таким образом, справедливость соотношений (2.2.28) доказана, причем их единственность следует из единственности разложения (2.2.30) вектора 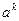 по базису
по базису 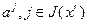 .
.
Перейдем к доказательству соотношения (2.2.29). Запишем:
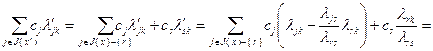
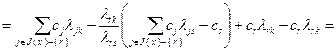
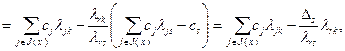 (2.2.31)
(2.2.31)
где 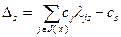 в соответствии с (2.2.9). Используя полученный результат (2.2.31), а также формулу (2.2.9), преобразуем второе выражение в (2.2.27):
в соответствии с (2.2.9). Используя полученный результат (2.2.31), а также формулу (2.2.9), преобразуем второе выражение в (2.2.27):
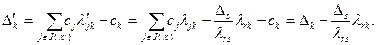
Таким образом, подтверждена справедливость формулы (2.2.29). Теорема
доказана.
При решении малых и, соответственно, не слишком трудоемких задач линейного программирования возможно выполнение расчетов по симплекс-методу вручную. При этом удобно использовать таблицу (симплекс-таблицу). Проиллюстрируем применение симплекс-метода на следующем примере.
Пример 2.2.2
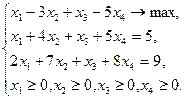
Здесь 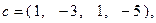
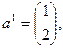
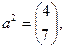
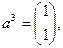
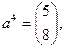
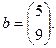
Первую опорную точку найдем с помощью метода, использованного в примере 2.2.1. Набору 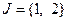 соответствует линейно независимая совокупность столбцов
соответствует линейно независимая совокупность столбцов 
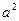 . В этом случае система (2.2.5) имеет вид:
. В этом случае система (2.2.5) имеет вид:
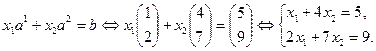
Ее решение 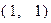 позволяет сформировать опорную точку
позволяет сформировать опорную точку 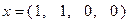 , при этом
, при этом 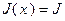 . Очевидно, что найденная опорная точка является невырожденной. На первом шаге (первой итерации) решения рассматриваемой задачи симплекс-таблица должна быть заполнена значениями величин, представленных в табл. 2.2.1. Сами значения показаны в соответствующих ячейках табл. 2.2.1а и получены следующим образом.
. Очевидно, что найденная опорная точка является невырожденной. На первом шаге (первой итерации) решения рассматриваемой задачи симплекс-таблица должна быть заполнена значениями величин, представленных в табл. 2.2.1. Сами значения показаны в соответствующих ячейках табл. 2.2.1а и получены следующим образом.
Таблица 2.2.1 Таблица 2.2.1а
 |  | 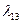 | 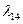 | 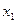 |
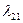 | 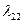 | 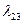 | 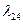 | 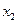 |
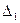 | 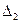 | 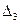 | 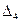 | 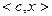 |
| 1 | 0 | -3 | -3 | 1 |
| 0 | 1 | 1 | 2 | 1 |
| 0 | 0 | -7 | -4 | -2 |
Вектор 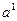 входит в базис
входит в базис 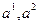 , поэтому коэффициенты его разложения по этому базису равны:
, поэтому коэффициенты его разложения по этому базису равны: 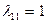 ,
, 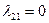 . Этот результат легко получить из системы уравнений
. Этот результат легко получить из системы уравнений
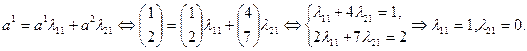
Аналогично для коэффициентов разложения вектора 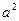 , также входящего в базис (
, также входящего в базис (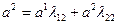 ), получаем
), получаем 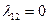 ,
, 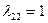 . В соответствии с (2.2.11)
. В соответствии с (2.2.11) 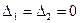 . Коэффициенты
. Коэффициенты 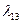 ,
, 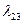 находим из системы:
находим из системы:
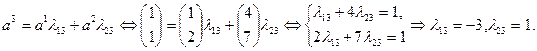
По формуле (2.2.9) вычислим значение 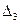 :
:
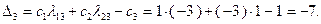
Определяем значения коэффициентов 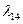 и
и 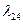 :
:
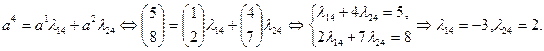
Находим значение 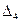 :
:
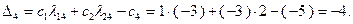
Значение целевой функции в рассматриваемой опорной точке 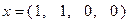 :
: 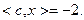
Анализ табл. 2.2.1а показывает, что выполнены условия теоремы 2.2.3. Для выполнения следующей итерации определим, используя выражение (2.2.22), значения величины 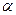 и индекса
и индекса 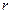 . В таблице имеется два отрицательных значения
. В таблице имеется два отрицательных значения 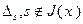 :
: 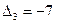 и
и 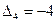 . Можно выбрать любое из них. Выберем
. Можно выбрать любое из них. Выберем 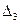 , соответственно
, соответственно 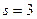 . В результате просмотра столбца табл. 2.2.1а от значения
. В результате просмотра столбца табл. 2.2.1а от значения 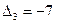 вверх находим единственное положительное значение
вверх находим единственное положительное значение 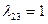 . Поэтому в данном случае при определении минимума в (2.2.22) нет альтернативы, следовательно:
. Поэтому в данном случае при определении минимума в (2.2.22) нет альтернативы, следовательно:
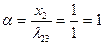 и
и 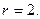
Используя (2.2.23), определим координаты следующей опорной точки:
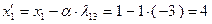 ;
; 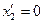 ;
; 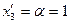 ;
; 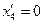 . Таким образом,
. Таким образом, 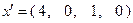 . В соответствии с теоремой 2.2.3,
. В соответствии с теоремой 2.2.3, 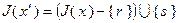 . Следовательно,
. Следовательно, 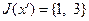 . На данном шаге симплекс-таблица должна быть заполнена значениями величин, представленных в табл. 2.2.2; сами значения приведены в табл. 2.2.2а. Значения в табл. 2.2.2а получены следующим образом. Зна-
. На данном шаге симплекс-таблица должна быть заполнена значениями величин, представленных в табл. 2.2.2; сами значения приведены в табл. 2.2.2а. Значения в табл. 2.2.2а получены следующим образом. Зна-
Таблица 2.2.2 Таблица 2.2.2а
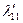 | 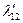 | 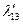 | 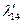 | 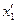 |
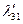 | 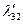 | 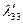 | 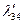 | 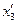 |
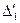 | 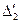 | 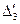 | 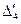 | 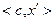 |
| 1 | 3 | 0 | 3 | 4 |
| 0 | 1 | 1 | 2 | 1 |
| 0 | 7 | 0 | 10 | 5 |
чения 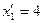 и
и 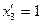 уже определены. Коэффициенты разложения векторов
уже определены. Коэффициенты разложения векторов 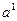 и
и 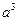 по базису, который из них и состоит, можно определить сразу:
по базису, который из них и состоит, можно определить сразу: 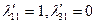 ;
; 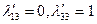 . Соответственно
. Соответственно 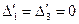 . Разумеется, такие же результаты для этих величин дает применение формул (2.2.28) и (2.2.29), по которым также рассчитаны значения 2-го и 4-го столбцов таблицы:
. Разумеется, такие же результаты для этих величин дает применение формул (2.2.28) и (2.2.29), по которым также рассчитаны значения 2-го и 4-го столбцов таблицы:
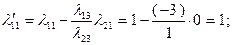
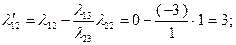
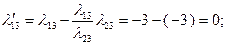
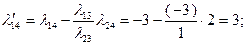
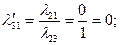
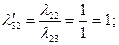
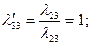
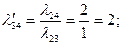
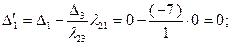
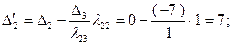
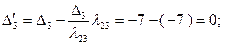
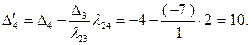
Значение целевой функции 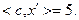 Поскольку
Поскольку 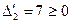 и
и 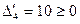 , выполнены условия теоремы 2.2.1 и, следовательно, точка
, выполнены условия теоремы 2.2.1 и, следовательно, точка 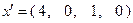 является решением задачи.
является решением задачи.
Работая с симплекс-таблицей, можно сократить объем вычислений. Заполнить строку новой таблицы – это значит получить вектор вида
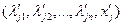 или вида
или вида 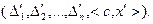 При получении вектора первого вида значения
При получении вектора первого вида значения 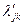 рассчитываются в соответствии с (2.2.28):
рассчитываются в соответствии с (2.2.28):
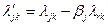 при
при 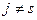 , где
, где 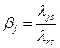 ,
, 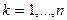 ;
; 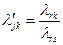 при
при 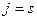 .
.
Используя (2.2.23), получаем, что при 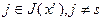
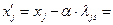
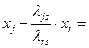
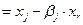 . При
. При 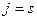
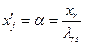 . Поэтому при
. Поэтому при 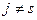 следует из строки
следует из строки 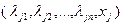 вычесть строку
вычесть строку 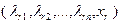 , умноженную на некоторое число (
, умноженную на некоторое число (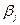 ), такое, чтобы на
), такое, чтобы на 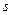 -м месте новой строки получился нуль. При
-м месте новой строки получился нуль. При 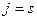 следует разделить строку
следует разделить строку 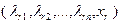 на некоторое число (
на некоторое число (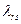 ), такое, чтобы на
), такое, чтобы на 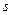 -м месте новой строки получить единицу. При получении вектора второго вида (последней строки новой таблицы) воспользуемся формулой (2.2.29), которую запишем в виде:
-м месте новой строки получить единицу. При получении вектора второго вида (последней строки новой таблицы) воспользуемся формулой (2.2.29), которую запишем в виде:
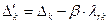 , где
, где 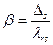 .
.
Для вычисления значения целевой функции используем формулу (2.2.21), преобразовав ее следующим образом:
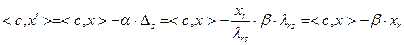 .
.
Таким образом, вычисление последней строки новой симплекс-таблицы заключается в вычитании из последней строки старой таблицы ее строки 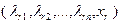 , умноженной на некоторое число (
, умноженной на некоторое число (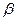 ), такое, чтобы на
), такое, чтобы на 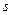 -м месте новой строки получился нуль. Из этого следует, что способ получения строки второго вида ничем не отличается от способа расчета строки первого вида при
-м месте новой строки получился нуль. Из этого следует, что способ получения строки второго вида ничем не отличается от способа расчета строки первого вида при 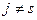 . Применение рассмотренного метода работы с симплекс-таблицей иллюстрирует следующий пример.
. Применение рассмотренного метода работы с симплекс-таблицей иллюстрирует следующий пример.
Пример 2.2.3
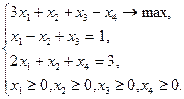
Здесь 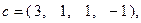
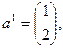
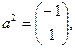
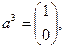
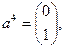
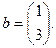
Для отыскания первой опорной точки рассмотрим набор 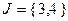 , которому соответствует линейно независимая совокупность столбцов
, которому соответствует линейно независимая совокупность столбцов 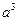 ,
, 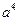 . В этом случае система (2.2.5) записывается в виде:
. В этом случае система (2.2.5) записывается в виде:
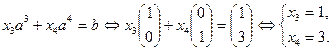
Полученное решение позволяет сформировать опорную точку 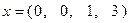 , при этом
, при этом 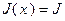 . Найденная опорная точка является невырожденной. На первом шаге решения данной задачи симплекс-таблица должна быть заполнена значениями величин, представленных в табл. 2.2.3. Сами значения приведены в соответствующих ячейках таблицы 2.2.3а и получены следующим образом.
. Найденная опорная точка является невырожденной. На первом шаге решения данной задачи симплекс-таблица должна быть заполнена значениями величин, представленных в табл. 2.2.3. Сами значения приведены в соответствующих ячейках таблицы 2.2.3а и получены следующим образом.
Таблица 2.2.3 Таблица 2.2.3а
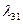 | 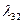 | 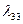 | 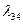 | 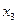 |
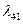 | 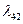 | 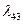 | 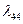 | 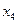 |
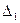 | 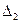 | 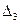 | 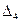 | 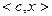 |
| 1 | -1 | 1 | 0 | 1 |
| 2 | 1 | 0 | 1 | 3 |
| -4 | -3 | 0 | 0 | -2 |
Коэффициенты разложения векторов 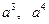 по базису, который из них состоит, записываем сразу:
по базису, который из них состоит, записываем сразу: 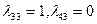 ;
; 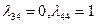 . В соответствии с (2.2.11)
. В соответствии с (2.2.11) 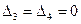 . Коэффициенты
. Коэффициенты 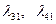 находим из системы:
находим из системы:
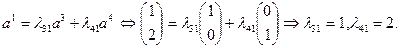
Используя формулу (2.2.9), найдем значение 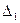 :
:
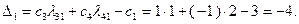
Получим значения 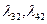 :
:
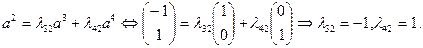
Находим значение 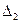 :
:
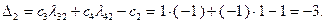
Значение целевой функции в рассматриваемой опорной точке 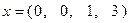 :
: 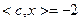 .
.
Из анализа табл. 2.2.3а следует, что выполнены условия теоремы 2.2.3. В таблице имеется два отрицательных значения 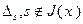 :
: 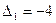 и
и 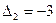 . Выберем
. Выберем 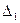 , тогда
, тогда 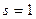 . В результате просмотра столбца табл. 2.2.3а от значения
. В результате просмотра столбца табл. 2.2.3а от значения 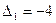 вверх находим два положительных значения:
вверх находим два положительных значения: 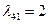 и
и 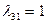 . Затем, используя (2.2.22), определяем значение индекса
. Затем, используя (2.2.22), определяем значение индекса 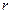 :
:
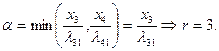
Таким образом, используемый на следующей итерации новый базис формируется из старого путем замены столбца 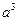 (так как
(так как 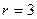 ) столбцом
) столбцом 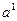 (так как
(так как 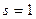 ). При этом в новой симплекс-таблице будут представлены коэффициенты разложения векторов
). При этом в новой симплекс-таблице будут представлены коэффициенты разложения векторов 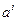 (
(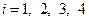 ) по новому базису. Состав новой симплекс-таблицы отражает табл. 2.2.4, а значения входящих в нее величин – табл. 2.2.4.а. Значения величин в табл. 2.2.4а получены следующим образом.
) по новому базису. Состав новой симплекс-таблицы отражает табл. 2.2.4, а значения входящих в нее величин – табл. 2.2.4.а. Значения величин в табл. 2.2.4а получены следующим образом.
Таблица 2.2.4 Таблица 2.2.4а
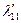 | 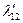 | 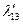 | 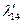 | 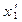 |
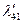 | 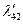 | 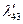 | 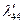 | 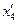 |
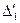 | 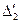 | 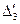 | 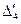 | 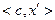 |
| 1 | -1 | 1 | 0 | 1 |
| 0 | 3 | -2 | 1 | 1 |
| 0 | -7 | 4 | 0 | 2 |
Поскольку 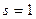 , а
, а 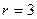 , первую строку табл. 2.2.4а получаем путем деления первой строки табл. 2.2.3а на число, которое обеспечит получение единицы на
, первую строку табл. 2.2.4а получаем путем деления первой строки табл. 2.2.3а на число, которое обеспечит получение единицы на 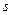 -м, т.е. на первом месте новой строки. Это число равно единице, поэтому в данном случае первые строки таблиц 2.2.3а и 2.2.4а совпадают. Вторая строка табл. 2.2.4а получена путем вычитания из второй строки табл. 2.2.3а ее первой строки, умноженной на такое число, которое обеспечивает получение нуля на
-м, т.е. на первом месте новой строки. Это число равно единице, поэтому в данном случае первые строки таблиц 2.2.3а и 2.2.4а совпадают. Вторая строка табл. 2.2.4а получена путем вычитания из второй строки табл. 2.2.3а ее первой строки, умноженной на такое число, которое обеспечивает получение нуля на 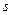 -м, т.е. на первом месте новой строки. Легко убедиться в том, что это число равно 2. Третья строка табл. 2.2.4а получена путем вычитания из третьей строки табл. 2.2.3а ее первой строки, умноженной на такое число, которое обеспечивает получение нуля на
-м, т.е. на первом месте новой строки. Легко убедиться в том, что это число равно 2. Третья строка табл. 2.2.4а получена путем вычитания из третьей строки табл. 2.2.3а ее первой строки, умноженной на такое число, которое обеспечивает получение нуля на 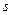 -м, т.е. на первом месте третьей строки новой таблицы. Это число равно –4. Опорная точка, полученная на данной итерации:
-м, т.е. на первом месте третьей строки новой таблицы. Это число равно –4. Опорная точка, полученная на данной итерации: 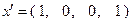 .
.
Анализ полученной табл. 2.2.4а показывает, что условия теоремы 2.2.3 выполнены и поэтому возможна очередная итерация. В последней строке таблицы имеется одно отрицательное значение 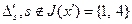 :
: 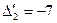 . Поэтому
. Поэтому 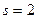 . В результате просмотра столбца таблицы от значения
. В результате просмотра столбца таблицы от значения 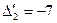 вверх находим одно положительное значение:
вверх находим одно положительное значение: 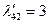 . Следовательно,
. Следовательно, 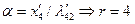 . Поэтому очередной новый базис формируется из предыдущего путем замены столбца
. Поэтому очередной новый базис формируется из предыдущего путем замены столбца 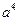 (так как
(так как 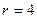 ) столбцом
) столбцом 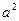 (так как
(так как 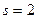 ).
).
Состав величин, характеризующий содержание очередной симплекс-таблицы, отражает табл. 2.2.5. Значения этих величин, представленные в табл. 2.2.5.а, получены следующим образом. Поскольку 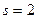 , а
, а 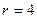 , первая строка табл. 2.2.5а получена путем вычитания из первой строки табл. 2.2.4а ее второй строки, умноженной на такое число, которое обеспечивает получение нуля на
, первая строка табл. 2.2.5а получена путем вычитания из первой строки табл. 2.2.4а ее второй строки, умноженной на такое число, которое обеспечивает получение нуля на 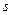 -м, т.е. на втором месте новой строки. Это число равно
-м, т.е. на втором месте новой строки. Это число равно 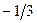 . Вторая строка табл. 2.2.5а получена в результате деления второй строки табл. 2.2.4а на число, обеспечивающее получение единицы на
. Вторая строка табл. 2.2.5а получена в результате деления второй строки табл. 2.2.4а на число, обеспечивающее получение единицы на 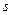 -м, т.е. на втором месте новой строки. Это число равно
-м, т.е. на втором месте новой строки. Это число равно 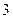 . Наконец, третья строка табл. 2.2.5а получена путем вычитания из третьей строки табл. 2.2.4а ее второй строки, умноженной на число, при котором обеспечивается получение нуля на
. Наконец, третья строка табл. 2.2.5а получена путем вычитания из третьей строки табл. 2.2.4а ее второй строки, умноженной на число, при котором обеспечивается получение нуля на 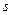 -м, т.е. втором месте новой строки. Требуемый результат получается при использовании числа
-м, т.е. втором месте новой строки. Требуемый результат получается при использовании числа 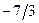 . Опорная точка, по лученная на данной итерации:
. Опорная точка, по лученная на данной итерации: 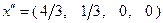 .
.
Таблица 2.2.5 Таблица 2.2.5а
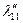 | 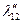 | 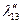 | 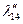 | 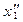 |
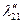 | 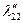 | 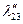 | 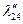 | 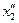 |
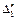 | 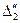 | 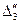 | 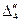 | 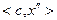 |
| 1 | 0 | 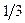 | 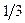 | 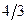 | |
- 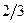 | 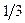 |
 Сейчас читают про:
|
 2015-04-01
2015-04-01 2003
2003







