Задача линейного программирования – это задача математического программирования, в которой целевая функция и функции, используемые в ограничениях, являются линейными. Основная задача линейного программирования записывается в виде:

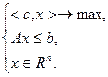 (2.1.1)
(2.1.1)
Здесь целевая функция 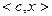 представляет собой скалярное произведение
представляет собой скалярное произведение
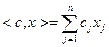 (2.1.2)
(2.1.2)
векторов 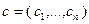 и
и 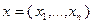 ,
,  – матрица размерности
– матрица размерности 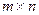 :
:
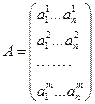 , (2.1.3)
, (2.1.3)
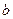 – вектор-столбец:
– вектор-столбец: 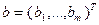 (T – символ транспонирования),
(T – символ транспонирования),
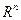 – n -мерное вещественное линейное пространство. Векторы
– n -мерное вещественное линейное пространство. Векторы 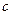 ,
, 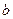 и матрица
и матрица 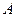 известны. Требуется найти хотя бы один вектор
известны. Требуется найти хотя бы один вектор 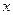 , принадлежащий допустимому множеству
, принадлежащий допустимому множеству 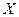 задачи (2.1.1)
задачи (2.1.1)
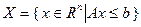 ,
,
доставляющий максимум функции (функционалу) 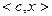 .
.
В дальнейшем (в зависимости от контекста) наряду с термином «вектор x» будет также использоваться термин «точка x», так как координаты точки x совпадают с координатами вектора, проведенного в эту точку из начала координат, а именно такие вектора и будут иметься в виду.
Помимо варианта записи задачи (2.1.1) существуют другие способы формулировки задач линейного программирования. Так называемая стандартная задача линейного программирования записывается в виде:
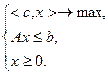 (2.1.4)
(2.1.4)
Существует также каноническая задача линейного программирования. Ее формулировка имеет вид:
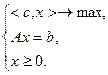 (2.1.5)
(2.1.5)
В выражениях (2.1.4), (2.1.5) условие 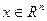 отсутствует, однако подразумевается как само собой разумеющееся. Покажем, что постановки (2.1.1), (2.1.4) и (2.1.5) можно свести одну к другой. Сначала преобразуем (2.1.4) и (2.1.5) к виду (2.1.1), затем (2.1.1) – к виду (2.1.4), а (2.1.4) – к виду (2.1.5). Из этого будет следовать, что (2.1.1) сводится к виду (2.1.5).
отсутствует, однако подразумевается как само собой разумеющееся. Покажем, что постановки (2.1.1), (2.1.4) и (2.1.5) можно свести одну к другой. Сначала преобразуем (2.1.4) и (2.1.5) к виду (2.1.1), затем (2.1.1) – к виду (2.1.4), а (2.1.4) – к виду (2.1.5). Из этого будет следовать, что (2.1.1) сводится к виду (2.1.5).
В задаче (2.1.4) условие 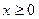 запишем в виде
запишем в виде 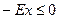 , где
, где 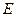 – единичная матрица размерности
– единичная матрица размерности 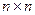 . Сформируем матрицу
. Сформируем матрицу 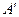 размерности
размерности 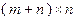 и вектор
и вектор 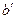 размерности
размерности 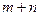 :
:
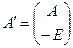 ,
, 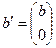 .
.
Тогда задача (2.1.4) запишется в виде, представляющем собой полную аналогию задачи (2.1.1):
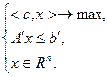 (2.1.6)
(2.1.6)
В задаче (2.1.5) условие 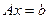 представим в виде системы неравенств:
представим в виде системы неравенств:
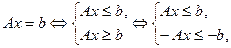
а условие 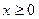 – в виде
– в виде 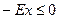 . Сформируем матрицу
. Сформируем матрицу 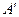 размерности
размерности 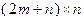 и вектор
и вектор 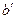 размерности
размерности 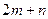 :
:
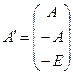 ,
, 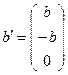 .
.
В результате задача (2.1.5) примет вид (2.1.6), т.е. будет сформулирована в виде основной задачи (2.1.1).
Теперь покажем, как основная задача (2.1.1) сводится к стандартной, т.е. к виду (2.1.4). Представим вектор 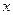 в задаче (2.1.1) в виде разности векторов
в задаче (2.1.1) в виде разности векторов 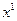 и
и 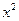 :
:
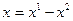 ,
, 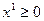 ,
, 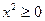 ,
, 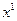 ,
, 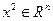 .
.
Запись 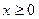 означает, что все
означает, что все 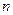 координат вектора
координат вектора 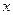 неотрицательны. Тогда задача (2.1.1) запишется в виде:
неотрицательны. Тогда задача (2.1.1) запишется в виде:
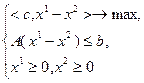
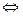
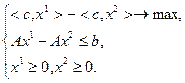 (2.1.7)
(2.1.7)
Введем матрицу 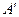 размерности
размерности 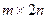 , а также векторы
, а также векторы 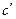 и
и 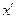 , размерность каждого из которых равна
, размерность каждого из которых равна 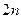 :
:
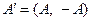 ,
, 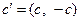 ,
, 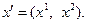
Это позволяет записать задачу (2.1.7) в виде:
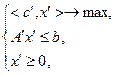
что полностью соответствует стандартной задаче (2.1.4).
Теперь рассмотрим, как стандартная задача (2.1.4) может быть сведена к канонической, т.е. к виду (2.1.5). Введем переменную 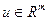 ,
, 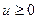 и запишем задачу (2.1.4) в виде:
и запишем задачу (2.1.4) в виде:
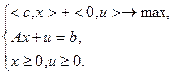 (2.1.8.)
(2.1.8.)
Далее введем матрицу 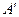 размерности
размерности 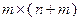 , а также векторы
, а также векторы 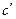 и
и 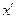 , каждый из которых имеет размерность
, каждый из которых имеет размерность 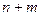 :
:
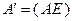 ,
, 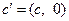 ,
, 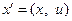 .
.
Тогда (2.1.8) примет вид:
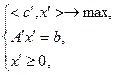
что полностью соответствует канонической задаче (2.1.5).
Пример 2.1.1. Привести к каноническому виду следующую задачу:
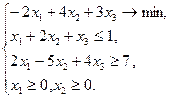
Сначала преобразуем задачу к стандартному виду. Для этого прежде всего перепишем ее в виде:
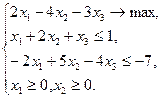
Очевидно, что в такой постановке задача не является стандартной, так как условие неотрицательности наложено не на все переменные. Введем две новые переменные 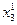 и
и 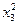 , принимающие неотрицательные значения. Тогда переменная
, принимающие неотрицательные значения. Тогда переменная 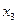 может быть представлена в виде:
может быть представлена в виде:
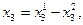
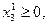
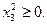
Заменив переменную 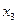 разностью новых переменных, получим задачу в стандартном виде:
разностью новых переменных, получим задачу в стандартном виде:
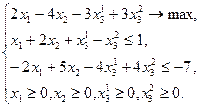
Для преобразования стандартной задачи введем две новые переменные: 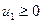 ,
, 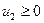 , с помощью которых получаем искомую каноническую задачу:
, с помощью которых получаем искомую каноническую задачу:
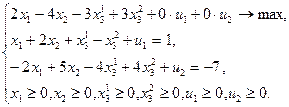
Рассмотрим задачу (2.1.5), в которой ранг r матрицы A (см. (2.1.3)) равен m. Если при этом выполнено условие 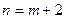 , то такую задачу можно решать геометрически. Для этого сначала необходимо выбрать две свободные переменные и выразить через них все остальные переменные. Например, если в качестве свободных переменных выбрать
, то такую задачу можно решать геометрически. Для этого сначала необходимо выбрать две свободные переменные и выразить через них все остальные переменные. Например, если в качестве свободных переменных выбрать 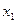 и
и 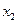 , то получим:
, то получим:
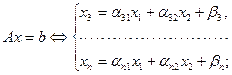 (2.1.9)
(2.1.9)
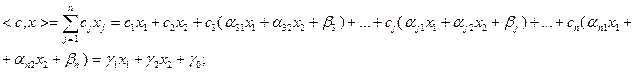
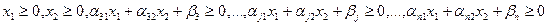 .
.
Числа 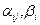 рассчитываются через элементы матрицы A и компоненты вектора b (
рассчитываются через элементы матрицы A и компоненты вектора b (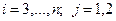 ), числа
), числа 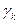 , кроме того, через компоненты вектора c (
, кроме того, через компоненты вектора c (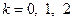 ). Таким образом, задача от n переменных сводится к задаче от двух переменных
). Таким образом, задача от n переменных сводится к задаче от двух переменных 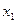 и
и 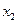 , решив которую, остальные переменные легко могут быть найдены по формулам (2.1.9).
, решив которую, остальные переменные легко могут быть найдены по формулам (2.1.9).
Запишем задачу в виде:
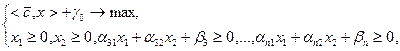 (2.1.10)
(2.1.10)
где 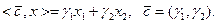
Покажем, что константу 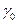 в задаче (2.1.10) можно не учитывать, так как
в задаче (2.1.10) можно не учитывать, так как
она влияет только на значение самого максимума, но не влияет на значение искомой точки максимума. Для этого рассмотрим задачу общего вида 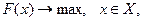 множество решений которой
множество решений которой
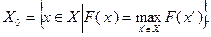
Рассмотрим также задачу 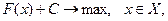 где
где 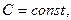 с множеством решений
с множеством решений 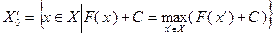 . Нетрудно убедиться в том, что
. Нетрудно убедиться в том, что 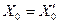 . Действительно,
. Действительно, 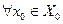 и
и 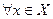 справедливо неравенство
справедливо неравенство 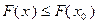 , которое равносильно неравенству
, которое равносильно неравенству 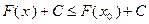 . Следовательно, каждый элемент множества
. Следовательно, каждый элемент множества 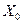 принадлежит множеству
принадлежит множеству 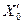 . Обратное утверждение доказывается аналогично. Итак, вместо задачи (2.1.10) можно решать задачу
. Обратное утверждение доказывается аналогично. Итак, вместо задачи (2.1.10) можно решать задачу
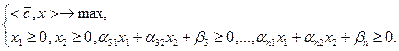 (2.1.11)
(2.1.11)
Решение 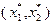 задачи (2.1.11) может быть найдено геометрическим методом, применение которого продемонстрируем на конкретном примере.
задачи (2.1.11) может быть найдено геометрическим методом, применение которого продемонстрируем на конкретном примере.
Пример 2.1.2
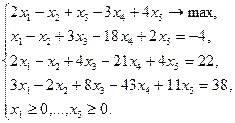
Данная задача является канонической,  ;
;
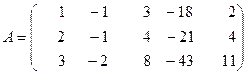 ,
, 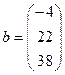 ,
, 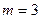 ,
, 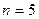 ,
,
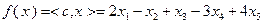 – целевая функция.
– целевая функция.
Выбрав 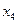 и
и 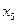 в качестве свободных переменных, из системы
в качестве свободных переменных, из системы  находим:
находим:
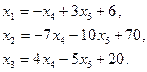 (2.1.12)
(2.1.12)
Подстановка этих выражений в целевую функцию дает:
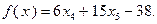
Отбросив константу -38, сформулируем задачу для двух переменных 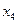 и
и 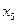 :
:
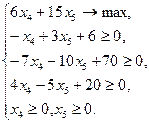 (2.1.13)
(2.1.13)
Неравенства в этой задаче образуют систему, графическое решение которой представляет собой пятиугольник ABCDE, показанный на рис. 2.1.1. Это и есть допустимое множество решений рассматриваемой задачи линейного программирования. Рассмотрим уравнение
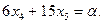 (2.1.14)
(2.1.14)
Для решения задачи (2.1.13) необходимо найти такое максимальное значение 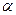 , при котором пересечение прямой (2.1.14) с допустимым множеством не пусто. В подобных задачах среди множества решений обязательно будет по крайней мере одна вершина многоугольника, представляющего собой допустимое множество решений задачи. При увеличении
, при котором пересечение прямой (2.1.14) с допустимым множеством не пусто. В подобных задачах среди множества решений обязательно будет по крайней мере одна вершина многоугольника, представляющего собой допустимое множество решений задачи. При увеличении 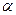 прямая (2.1.14) перемеща-
прямая (2.1.14) перемеща-






|
|
|
|
|



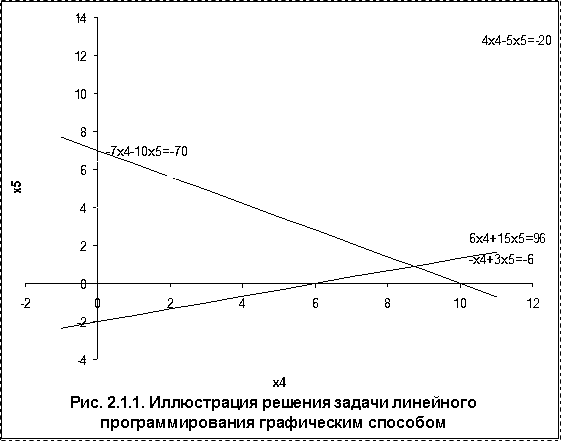
ется в направлении вектора с координатами (6,15), сохраняя ортогональность с этим вектором. На рис. 2.1.1 показано конечное положение прямой (2.1.14), при котором ее пересечение с пятиугольником ABCDE не пусто. Оно соответствует значению 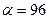 , при этом пересечением является точка C. Решением задачи (2.1.13) являются координаты точки C:
, при этом пересечением является точка C. Решением задачи (2.1.13) являются координаты точки C: 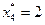 ,
, 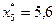 . Их подстановка в выражения (2.1.12) позволяет найти значения остальных координат искомого решения
. Их подстановка в выражения (2.1.12) позволяет найти значения остальных координат искомого решения 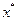 исходной задачи:
исходной задачи: 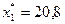 ,
, 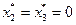 .
.
Запишем найденное решение в виде: 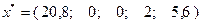 . При этом
. При этом 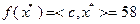 .
.
 2015-04-01
2015-04-01 756
756








