Тетраэдр топтары куб тобының топшалары болып табылады, яғни тетраэдр симметриясының түрленулері куб симметриясының түрленуінің жиынтығы болып саналады. GaAs, InSb кристалдарының симметриясы тетраэдр болып келеді. 1.10-суретте кубтың ішіндегі тетраэдр көрсетілген. Тетраэдрдің инверсия центрі жоқ екені көрініп тұр.
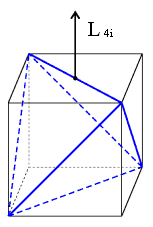 1.10 сурет.Тетраэдрсимметриясының өсі және симметрия жазықтығы 1.10 сурет.Тетраэдрсимметриясының өсі және симметрия жазықтығы |
Тетраэдр тобына мына түрленулер: E, 3L42, 4L3, 4L32 (12 қарапайым бұрылыс), 6 айналы бұрылыс: 3L4i, 3L4i2 және 6 жазықтықтағы шағылысу: 6P (симметрия жазықтығы тетраэдр қабырғасы арқылы өтеді) жатады. Тетраэдр тобы Td арқылы белгіленіп, құрамына 24 түрлену кіреді.
1.6. Кристалдың кеңістікті симметриясы
Осыған дейін біз симметрияның түрленуінің екі типін қарастырып келдік: трансляция және нүктелік түрленулер. Трансляцияға қатысты симметрия — кристалдың басты қасиеті. Оны толықтай Бравэ торы айшықтайды (2, 3-кестелерді, 1.9,1.10-суреттерді қара).
2-кесте. Бес екі өлшемді Бравэ торлары
| Торлар | Қарапайым ұяшық | Симметрияның нүктелік тобының халықаралық көрсеткіші |
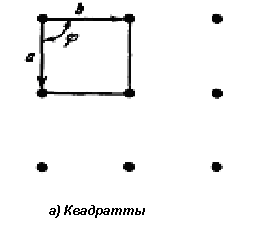
| Қиғаш бұрышты | Параллелограмм 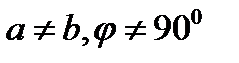 | |
| Квадратты | Квадрат, 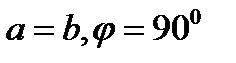 | 4mm |
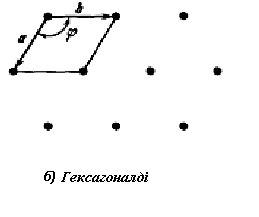
| Гексагональді | 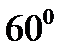 -градусты ромб, -градусты ромб, 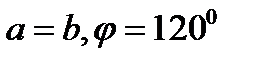 | 6mm |
| Тікбұрышты | Тікбұрышты, 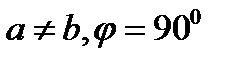 | 2mm |
| Центрленген тікбұрышты | Тікбұрышты, 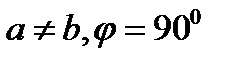 | 2mm |
· mm көрсеткіші екі жазықтықтың айналы шағылысуы бар екендігін көрсетеді
3-кесте. Он төрт кеңістікті Бравэ торы
| Кристаллографиялық жүйе (сингония) | Жүйедегі ұяшық саны | Ұяшық символы | Элементар ұяшықтың сипаттамасы |
| Триклинді | P | 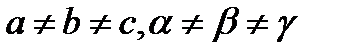 | |
| Моноклинді | P, C | 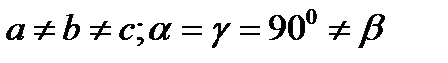 | |
| Ромбты | P, C, I, F | 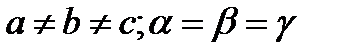 = = 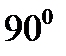 | |
| Тетрагоналді | P, I | 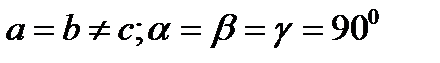 | |
| Кубты | P, I, F | 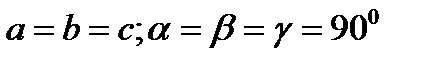 | |
| Тригоналді | R | 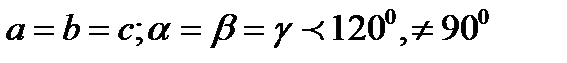 | |
| Гексагоналді | P | 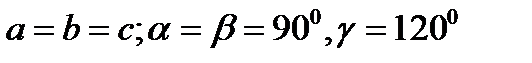 |
Суретте көрсетілген қарапайым ұяшықтардың барлығы примитивті емес. С - бұл центрлі негізі бар болатын ұяшық, I - көлемді-центрленген ұяшық, F- қырға центрленген ұяшық.
3-кестеде торлардың типтері, ал 12-суретте он төрт кеңістікті Бравэ торлары көрсетілген.
 |  |
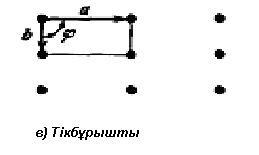 | 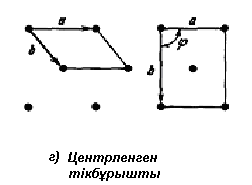 |
1.11-сурет. Бес екіөлшемді Бравэ торы
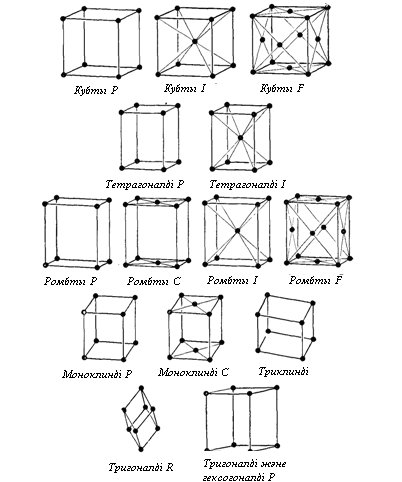
1.12-сурет. Он төрт кеңістікті Бравэ торлары
Браве торының симметриясы нүктелік түрленулерге қатысты сингония немесе кристалды жүйе деп аталады. Түрлі сингонияны сипаттайтын симметрияның барлығы 7 тобы бар (3-кесте), яғни 7 түрлі топтың әрқайсысында нақты бір Бравэ торының симметрияның барлық нүктелік түрленулері болады. Кристалл трансляциялық симметриясын толықтай анықтайтын Бравэ торымен ғана емес, сонымен қатар базиспен, яғни примитивті ұяшықтың түзілуімен (примитивті ұяшықты құратын атомдардың типтері мен келісімді орналасуы) де сипатталады. Бравэ торының әр түйініне бір атом сәйкес келетін, қарапайым кристалл симметриясы Бравэ торының сингониясымен сәйкес келеді. Ал күрделі кристалға келетін болсақ, онда оның нүктелік симметриясы Бравэ торының симметриясынан жоғары бола алмайды. Осылайша, жалпы жағдайда кристалдың нүктелік симметриясының тобы оның Бравэ торының (сингония) симметрия тобының топшалары болып келеді. Осындай топшаларды, яғни трансляциялық симметриямен сәйкес келетін нүктелік симметрия тобы 32 – ге жетеді.
Мысалы, Oh кубының симметрия тобының (кубты сингония) бес топшасы бар, оның ішінде біз қарастырған үш топтар да бар: Oh, O, Td.
Нүктелік түрленулер мен трансляциялар кристалдық тор симметриясының түрлену жиынын жояды (олар Бравэ торының симметриясының түрленуін де жояды).
Кристалдық торлардың қосымша симметрия элементтері де бола береді:
n-ші ретті бұрандалы өстер. Сәйкес түрленулер бұрыштарға бұрылуға және дәл осы оспен pa/n арақашықтығына жеткізілуіне негізделген. Мұнда p=1,2,...,n–1; a — нақ осы осьтегі ең аз период.
Айналы сырғу жазықтығы. Сәйкес түрленулер ось бойымен жүретін трансляцияның нақ сол жазықтықта a/2 арақашықтықта жататын осы жазықтыққа шағылысуына негізделген.
Кристалдың кеңістікті симметрия тобы кристалдық тордың симметриясының барлық түрленулерін қамтиды: трансляция, нүктелік түрленулер, бұрандалы өстер мен айналы сырғу жазықтығына байланысты түрленулер (кристалдық тордың симметриясының басқа түрленулері болмайтындығын көрсетуге болады). Симметрияның барлық кеңістікті топтары XIX ғасырдың аяғында Е.С.Федоровпен табылған. Олардың саны 230.
1.7. Кристалографиялық индицирлеу әдісі. Бүтін сандар заңы.
Кристалдық тор қарапайым ұяшықтың алты параметрлерімен: 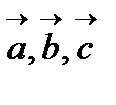 қабырғаларының ұзындығы және
қабырғаларының ұзындығы және 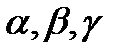 бұрыштарымен сипатталады. Кристалдық құрылым мен көпжақтыларды сипаттау үшін кристаллографиялық индицирлеу әдісін қолданады. Ол координаталардың барлық кристаллографиялық жүйелері үшін ыңғайлы. Осы әдісті қарастырып көрейік.
бұрыштарымен сипатталады. Кристалдық құрылым мен көпжақтыларды сипаттау үшін кристаллографиялық индицирлеу әдісін қолданады. Ол координаталардың барлық кристаллографиялық жүйелері үшін ыңғайлы. Осы әдісті қарастырып көрейік.
Түйіндердің символы.Егер тордың бір түйінін координаталар басы деп таңдап алсақ, онда тордың кез-келген басқа түйіні мына түрде анықталады:
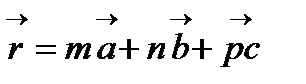 (1.1)
(1.1)
Мұндағы m,n,p – үш сан, берілген түйіннің индексі деп аталады. Екі жақша [[mnp]] түрінде жазылған m,n,p сандарының жиынтығы түйін символы деп аталады. Символдағы сандар үтірсіз, бірінен соң бірі жазылады, оқылғанда жеке-жеке айтылып кетеді. Минус таңбасы санның үстіне қойылады.
Бағыт пен қатар (қабырға) символдары.Тордағы қатар мен түйін сызығы, онымен қоса кристалдық көпжақтардың қабырғалары таңдалып алынған координата жүйесінде еңкеюмен сипатталады. Егер қатар координата басы арқылы өтпесе, онда біз оны әрқашан паралельді түрде өткізе аламыз, өйткені кристалдағы барлық параллель бағыттар бірдей. Онда қатардың бағыты екі нүкте арқылы анықталады: координаталар басы және қатардың кез-келген түйіні. Бұл түйін символы қатар символының орнына алынып, квадрат жақша [mnp] түрінде жазылады. Бұл символ параллель қатарлардың тұқымдасын сипаттайды.
Параллель қабырға арқылы қиылысатын кристалл қырлары белдеу немесе зонаны құрады, ал осы қабырғалардың жалпы бағыты зона өсі деп аталады.
Айқындық үшін қатар символы орнына координаталар басына жақын орналасқан түйін таңдалынады. Егер символдағы индекстер қалдықсыз болса онда оларды қысқартуға болады.
Жазықтық (қырлар) символдары.Қандай да бір жазықтық ma, nb, pc кесінділерінің үш кристаллографиялық өстерін қиып өтсін делік. m:n:p қатынасы жазықтықтың координата осіне қарай иілуін сипаттайды. Параллель жазықтығының барлық тұқымдастарының орналасуы осындай қатынаспен анықталады. Барлық параллель жазықтық үшін рационалды сандар m:n:p қатынасының сериясын Вейсс парметрлері деп аталатын, бүтін қарапайым бөлшектердің өзара p:q:r қатынасы түрінде қарастыруға болады. Кристаллографияда жазықтарды параметрлермен емес Миллер индексімен сипаттайды. Миллер индексі бүтін сандарға келтірілген және Вейсс параметрлеріне кері шама. Егер жазықтықтардың параметрлері p, q, r болса, онда Миллер индексі мына қатынас арқылы анықталады:
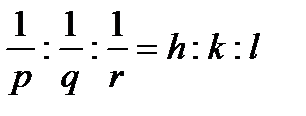 (1.2)
(1.2)
h, k, l - сандары жазықтық индекстері деп аталады. Индекстер бірінен соң бірі жақшаның ішіне (hkl) жазылады. (hkl) символдары барлық параллель жазықтардың жиынтығын сипаттайды (11-суретті қара).
Координата өстерінің символдары өстер арасындағы бұрыштарға тәуелсіз әрқашан: XOY =(001), XOZ = (010), YOZ = (100) болады.
Индекстер және символдар арқылы кристалдардың қырлары мен қабырғаларын сипаттау әдістері бұрын, қристалдың торлы құрылымы тәжірибе жүзінде дәлелденбей тұрып, қалыптасқан болатын. Ол кристаллографияның эмпирикалық заңы – бүтін сандар заңына негізделген.
Бүтін сандар заңы. Заңды 1819 жылы Гаюи ашты. Координаталар өсіне кристалдық көпжақтының үш параллель емес қабырғалар бағытын таңдап аламыз, ал осы өстер бойынша өлшем бірліктеріне (параметрлерге) – бірлік ретінде қабылданған, оған кристалдың қандай да бір қабырғасы арқылы өтетін кесіндіні аламыз. Бірлік қабырға ОА, ОВ,ОС кесінділерін координата осьтерінде басып өтеді деп есептейік. Бүтін сандар заңы мынаны тұжырымдайды: нақты кристалдың кез-келген екі қыры үшін параметрлерінің екілік қатынасы бүтін сандар қатынасына тең болады, яғни.
ОА*/OA = OB*/OB = OC*/OC = p:q:r (1.3)
Мұндағы p, q, r – бүтін, қарапайым сандар және нақты кристалдар үшін оның шамасы төмен, 5-тен артылмайды. А*В*С* жазықтығы кристалл қыры бола алады егер, координата осьтерінде оларды басып өтетін ОА*, ОВ*, ОС* және ОА, ОВ, ОС бірлік кесінділері (1.2) қатынасының кесінділерін сәйкес болса. Нақты кристалдарда (1.3) қатынасы иррационал болатын қырлар мүмкін болмайды
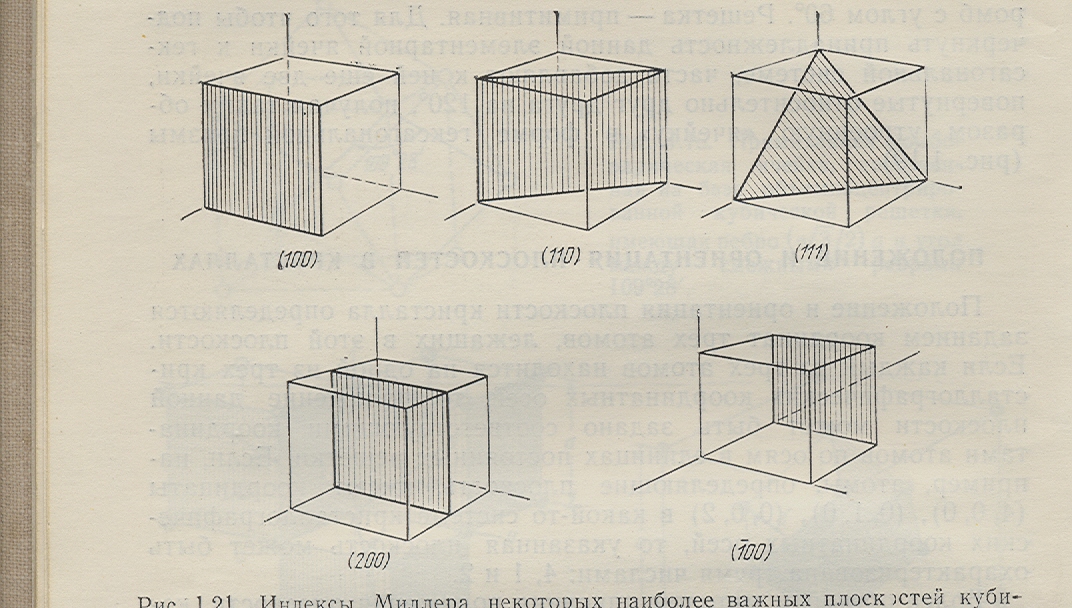
1.13-сурет. Кубты кристалдағы маңызды жазықтар үшінМиллер индексі
Кез-келген кристаллографиялық жазықтықтың Миллер индексін табу үшін ең алдымен координаталар басын таңдап алу керек, сосын координаталар өсінде, а, b, c, өсті кесінділері арқылы өтетін жазықтықпен кесетін кесінділерін көрсету керек, одан ары осы шамалардың кері мәндерін тауып, жалпыға бірдей алымы бар, мүмкін болатын ең кіші рационалды бөлшек түріне келтіру керек, және соңында жалпыға бірдей алымын шығарып тастап, алынған үш санды жақшаға алу керек.
Миллер индексін анықтайтын бірнеше мысалдарды қарастырайық.
1. Координата өсінде 4a, 3b, 2c қиындыларын қиып өтетін жазықтық символдарын табу керек. m:n:p = 4:3:2 қатынасын жазамыз:
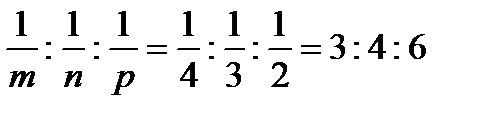
Яғни, жазықтық символы (hkl)=(346).
2. X және Z остеріне параллель және Y осінде үш бірлікке қиылысатын Миллер индексін табу керек
m:n:p= 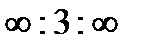 болсын
болсын
Осыдан
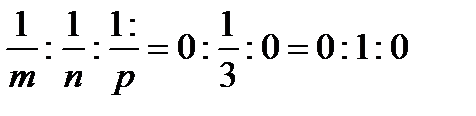 яғни (hkl)=(010)
яғни (hkl)=(010)
Координаталар өсін және жеке қырларын таңдау үшін қондырғылардың шартты халықаралық ережелері (№1 зертханалық жұмысын қара) бар. Рентгендіқұрылымды талдау арқылы қарапайым ұяшықтардың құрылымын, пішінін және параметрлерін, сәйкесінше рентгенограмма және олардың проекциясы арқылы жазықтық символдары мен бағыттарын анықтауға болады. Кристалдық көпжақтылардың қабырғалары мен қырларын да кристаллографиялық проекция арқылы анықтау ыңғайлы (№1 зертханалық жұмысты қара).
1.8. Қарапайым кристалдық құрылымдар
Хлорлы натрий құрылымы.Қарапайым кристалдық құрылым -ас тұзы NaCl. Бравэ торы қырға центрленген кубты тор: үшінші ретті төрт өсі бағыты жағынан қарапайым ұяшықтың ала диагоналымен сәйкес келеді, жазықтық симметриясы m координатты және диагональді бағытта өтеді, кеңістікті тобы Fm3m болады. Базис Na-дің бір атомынан және CI-дың бір атомынан тұрады, олардың арақашықтығы қарапайым куб жазықтығының диагоналының жартысына тең. Қарапайым куб төрт NaCl молекулаларынан тұрады. Атомдардың келесідей координаталары бар:
Na: 000; 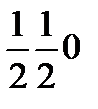 ;
; 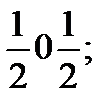
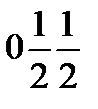 ;
;
Cl: 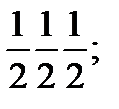 00
00 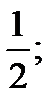 0
0 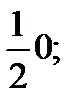
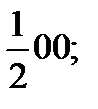
Әрбір атомның алты жақын орналасқан, бірақ басқа атом сорты болып келетін көршілері болады
4-кесте. NaCl типтес құрылымы бар кристалдардың өкілдері:
| Кристалл | а.А А | Кристалл | а.А |
| LiH | 4,08 | AgBr | 5,77 |
| PbS | 5,92 | KBr | 6,59 |
а- кристалдық тордың тұрақтысы, ангстреммен берілген. Суретте PbS кристалы көрсетілген, оның пішіні куб тәрізді.
Хлорлы цезий құрылымы.Хлорлы цезий құрылымында бір қарапайым ұяшыққа бір молекула келеді. Базис координатасы 000 болатын Cs-дің бір атомынан және координатасы 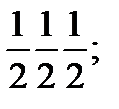 болатын Cl-дың бір атомынан тұрады.
болатын Cl-дың бір атомынан тұрады.
Кеңістіктік торы – көлемді-центрленген қарапайым кубты. Кубтың центрі болып табылатын әрбір атомның куб бұрыштарында орналасқан көршілері координациялық саны сегізге тең басқа атом сортынан болады.
5-кесте. CsCl типтес құрылымы бар кристалдардың өкілдері:
| Кристалл | a, A | Кристалл | a, A |
| CsCl | 4,11 | CuZn (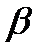 ) )  -латупь) -латупь) | 2,91 |
| CuPd | 2,99 | BeCu | 2,70 |
Мұндағы CuZn (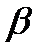 )-латуннің модификациясы.
)-латуннің модификациясы.
Тығыз орналасқан гексагоналді құрылым. Қатты шариктер түріндегі атомдардың тығыз орамасын қарастырайық.
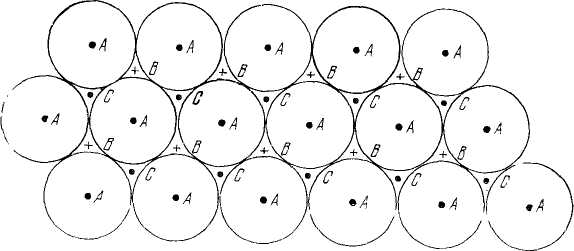
1.14-сурет. Шарлардың тығыз орналасқан беті.
1.14-суретте тығыз орналасқан қабаттар көрсетілген. Шарлардың центрлері А нүктелерімен белгіленген. Екінші беттің шарларын бірінші беттегі шарлардың үстіне олардың центрлері В орнына түсетіндей етіп орналастыруға болады (немесе, С-ның орналасуына эквивалент). Егер екінші беттің шарлары В орнына түссе, онда үшінші беттің шарларының орналасуын екі жолмен жүзеге асыруға болады, яғни А – ның немесе С – ның үстіне орналастыру арқылы. Бірінші жағдайда беттердің АВАВАВ.... тізбегін аламыз және құрылымы тығыз орамасы бар гексагоналді құрылымболып келеді. Екінші жағдайда беттердің ABCABC'ABC.. тізбегін аламыз, ал құрылымы тығыз орамасы бар қырға центрленген кубты құрылым болады. Тығыз ораманың жазықтығы болып 13-суретте көрсетілгендей (111) жазықтығы табылады.
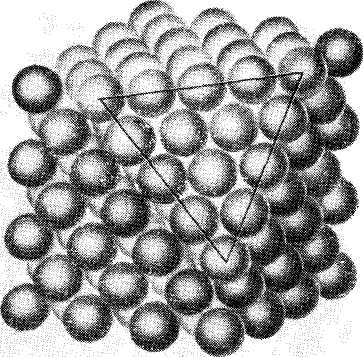 |
1.15-сурет. Қырға центрленген кубты құрылым. (111) жазықтығын көрсету үшін бір бұрышы кесіліп алынған. (111) жазықтығы қатты шарлардың тығыз орналасқан қабаттары болып табылады.
Тығыз орналасқан гексагоналді құрылым 1.14-суретте көрсетілген қатты шарлармен толтырылған көлемнің жартысы жалпы көлемнің 0,74-ін құрады және ол көрсеткіш тығыз орналасқан куб үшін де гексагоналді құрылым үшін де бірдей.
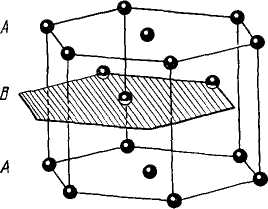
1.16-сурет. Тығыз орналасқан гексагоналді құрылым.
Осы құрылымдағы атомдардың орналасуы кеңістіктік торға жауап бермейді. Кеңістікті тор – бұл қарапайым гексагоналді тор, оның базисі тордың әр нүктесімен байланысты екі атомнан тұрады.
Тығыз орналасқан гексагоналді құрылымның қарапайым ұяшығы примитивті гексагоналді ұяшық болып табылады, ал оның базисі екі атомнан тұрады (1.16-суретке қара). Қырға центрленген кубты ұяшықтың ішінде таңдалған примитивті ұяшықтың бір ғана атомы бар.
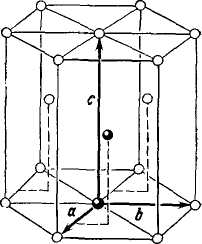 |
1.17-сурет. Примитивті ұяшық- а = b үшін а мен b арасындағы бұрыш 120° тең. с өсі а және b-да жатқан жазықтыққа перпендикуляр. Идеал тығыз орналасқан гексагоналді құрылым үшін с = 1,633а. Базис құратын екі атом суретте қара шариктермен белгіленген.
с/а қатынасының мәні тығыз орналасқан гексагоналді құрылым үшін (8/3)1/2 = 1,633 тең. с/а қатынасы теориялық мәнінен ерекшеленген жағдайда да кристалдарды тығыз орналасқан гексогоналді құрылымы бар кристалдар класына жатқызуға болады деп келіскенбіз. Осылай с/а = 1,86 (а = 2,66 А, с = 4,94 А) болатын цинкті де тығыз орналасқан гексогоналді құрылымы бар кристалл қатарына жатқызу керек, дегенмен оның құрылымындағы байланысқан атомдар арасындағы бұрыштары идеал тығыз орналасқан гексогоналді құрылымы бар кристалдардағы атомаралық бұрыштарға қарағанда айрықша ерекшеленеді. с/а қ атынасы — 1,623 болатын магнийдің тығыз орналасқан гексогоналді құрылымы идеал болып келеді.
Көптеген металлдар қандай да бір нақты температурада өз пішінін қырға центрленген кубты құрылымнан тығыз орналасқан гексогоналді құрылымға және кері айтарлықтай жеңіл өзгертеді. Атомдар санымен анықталатын және сол атомның жақын көршілері болып келетін координациялық сан тығыз орналасқан екі түрлі құрылым үшін де бірдей болатынын айтып кету керек. Егер байланыс энергиясы атом мен оның көршілері арасындағы байланыс санына тәуелді болса, онда қырға центрленген кубты құрылым мен гексогоналді тығыз орналасқан құрылымның энергиялары бірдей болар еді.
Гексогоналді тығыз орналасқан құрылымы бар кристалдардың мысалдарын 6-кестеден көруге болады.
6-кесте. Тығыз орналасқан гексагоналді құрылымы бар кристалдардың өкілдері
| с/а | Кристалл | c/a | Кристалл | Кристалл | c/а |
| 1,633 | Zn | 1,861 | Zr | Не | 1,594 |
| 1,581 | Cd | 1,886 | Gd | Be | 1,592 |
| 1,623 | Co | 1,622 | Lu | Mg | 1,586 |
| 1,586 | Y | 1,570 | Ti |
Төрт қатардан САВАСАВАС А, бес қатардан ВАВСАВАВСАВ А және т.с.с., тұратын тығыз орналасқан құрылымдар болатындығын айтып кетейік. Тығыз орналасқан көп 80 және одан жоғары қатардан тұратын құрылымдар белгілі. Қатарлардың саны артқан сайын әрбір n – қатардың мүмкін болатын орналасуы да артады.
Тығыз орналасу идеясы белгілі құрылымдарды суреттеу және жаңа құрылымдарды іздеу үшін маңызды орын алады. Бағытсыз байланыстары бар құрылымдар үшін тығыз орналасу әдетті жағдай.
Алмаздың құрылымы. Алмаздың кеңістікті торы гранецентрленген кубты. Тордың әр түйінімен, координаталары 000 және 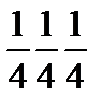 екі бірдей атомдардан тұратын, примитивті базис байланысты (1.18-сурет). Алмаз құрылымының кеңістікті тобы Fd3m; координаталық бағыттарда d (алмазды) типті сырғанау шағылу жазықтығында өтеді, ал диагональ бағыт бойынша - m типіндегі жазықтар өтеді. Олардың қиылысатын жерінде құйынды 41 өстері туады
екі бірдей атомдардан тұратын, примитивті базис байланысты (1.18-сурет). Алмаз құрылымының кеңістікті тобы Fd3m; координаталық бағыттарда d (алмазды) типті сырғанау шағылу жазықтығында өтеді, ал диагональ бағыт бойынша - m типіндегі жазықтар өтеді. Олардың қиылысатын жерінде құйынды 41 өстері туады
Алмаз құрылымында тетраэдрлік байланыстар 1.18-суретте көрсетілген сызбамен бейнеленеді. Әрбір атомның төрт өте жақын және олардан кейінгі он екі көршісі болады. Қарапайым кубтың сегіз атомы бар. Алмаздың торы тығыз орналасқандар қатарында жатпайды; қатты шарлармен толтырылған максималді қатысты көлем тек 0.34 құрайды, яғни тығыз орналасқан құрылымды сипаттайтын толтыру коэффициенті мәнінің шамамен 46% құрады.
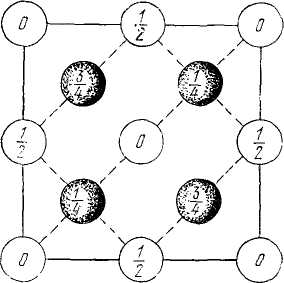 |
1.18-сурет. Алмаздың қарапайым кубты ұяшығында атомдардың орналасуы(куб қырына проекция). Бөлшектердің мәні атомдардың базисті жазықтығының үстінде орналасу биіктігін көрсетеді (бірлік ұзындығына кубтың қабырғасы сәйкес келеді). Биіктіктері 0 және 1/4 болатын нүктелер гранецентрленген кубты торды құрайды; биіктіктері 1/4 және 3/4 болатын нүктелер кубтың кеңістікте диагоналі бойынша, және оның ұзындығының төрттен бір бөлігіне қарай ығысқан дәл осындай торларды құрайды. Базис бірдей екі атомдардан тұрады.
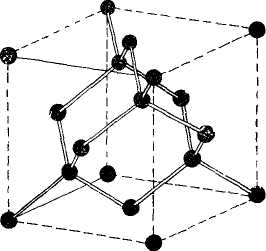 |
1.19-сурет. Байланыстардың тетраэдрлік орналасуын көрсететін алмаз кристалының құрылымы бейнеленген.
Алмаздың құрылымдық типінде сыртқы қарапайым жартылайөткізгіштер: германий, кремний, онымен қоса күкіртті қалайы.
1.9. Кері тор. Кері тордың қасиеттері. Бриллюэн зонасы. Вигнер-Зейтц ұяшығы. Кері тор.
Вигнер-Зейтц ұяшығы. Анықтама бойынша примитивті ұяшық бұл минимальді көлемді ұяшық. Кристалдың бір примитивті ұяшығына тордың тек бір түйіні ғана сәйкес келеді. Примитивті ұяшық Вигнер-Зейтц ұяшығы түрінде жиі кездеседі. Вигнер-Зейтц ұяшығын құру келесідей болады: тордың бір түйіні таңдалып алынады, осы түйінді басқа көрші түйіндермен жалғайтын сызық жүргізіледі. Құрылған сызықтың ортасы арқылы оған перпендикуляр жазықтық жүргізіледі. Осы жазықтықпен шектелген фигура Вигнер-Зейтц ұяшығы болып табылады.
Кері тор. Рентгенді дифракцияда кері тор ұғымы қолданылады. Кері тордың негізгі (базисті) векторлары төмендегі теңдеулермен анықталады:
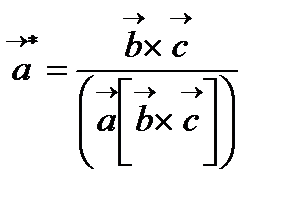 ;
; 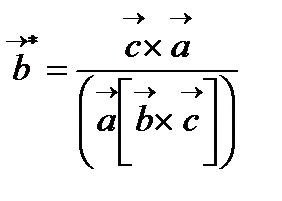 ;
; 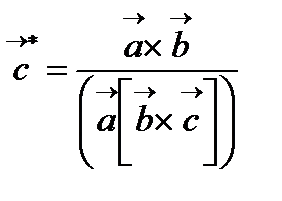
Мұнда векторлық алгебрада төмендегі қатынас орындалатындығы көрсетілген:
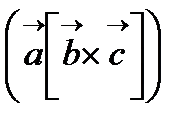 =
= 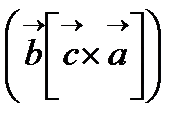 =
= 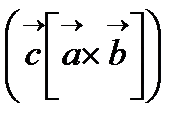
Алымында тұрған шама қарапайым ұяшықтың көлемін көрсетеді.
Кері торлардың бұрыштық параметрлері мына теңдеумен анықталады:
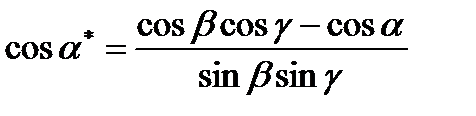 ;
; 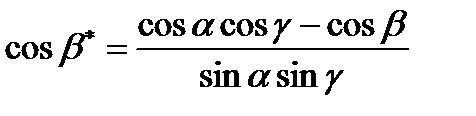 ;
; 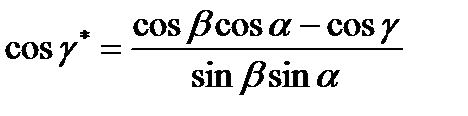 .
.
Кері тордың трансляция векторы:
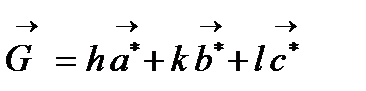 ,
,
мұндағы h,k,l –бүтін сандар.
Кері тордың трансляция векторының тура тордың трансляция векторына көбейтіндісі:
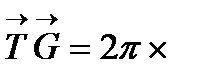 бүтін сандар
бүтін сандар
Кристаллографтар әдетте 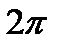 көбейткішін түсіріп тастайды, бірақ конденсирленген күй физикасымен айналысатын физиктердің көпшілігі осы көбейткішті қалдырады.
көбейткішін түсіріп тастайды, бірақ конденсирленген күй физикасымен айналысатын физиктердің көпшілігі осы көбейткішті қалдырады.
Әрбір кристалдық құрылымға екі тор: кристалдық тор және кері тор сәйкес келеді. Олар жоғарыда көрсетілген қатынастармен тығыз байланысты. Кристалдың рентгендік дифракциялық суреті кері тордың картасын берсе, микроскопиялық суретте кристалдың нақты құрылымының картасын дәл солай береді деуге болады. Кристалдық тор векторының ұзындық өлшемі болса, кері тор векторының шамасы [ұзындық]-1.
Кристалдық тор – бұл әдетте нақты кеңістікте кездеседі, ал кері тор – бұл Фурье кеңістігіндегі тор. Бриллюэннің бірінші зонасы ол кері тордағы Вигнер-Зейтц ұяшығы.
Кері тордың көмегімен кристаллографияның көптеген міндеттері жеңіл шешіледі. Кристаллографиялық есептеулерде жиі кездесетін бірнеше теңдеулерге мысал келтірейік. (hkl) жазықтығы сериясы үшін жазықтықтар арасындағы қашықтықтар мына теңдеу арқылы анықталады:
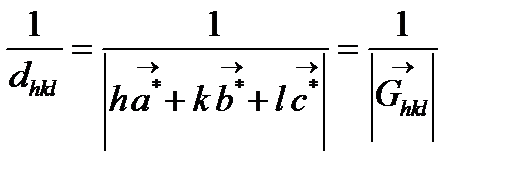
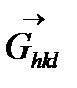 векторының ұзындығы мына формуламен есептеледі:
векторының ұзындығы мына формуламен есептеледі: 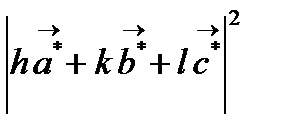 . Осылай гексагоналді сингония үшін:
. Осылай гексагоналді сингония үшін:
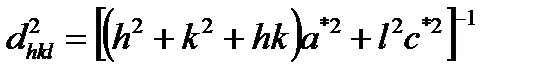 ,
,
мұндағы 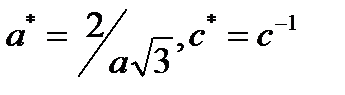 . Кубты тор үшін:
. Кубты тор үшін:
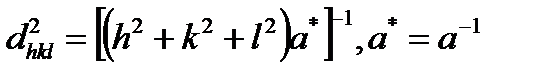 .
.
 2015-04-01
2015-04-01 2884
2884








