Симплексный метод, или метод последовательного улучшения решения, универсален, им можно решить любую ЗЛП.
Пусть ЗЛП задана в канонической форме:
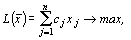 (1)
(1)
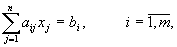 (2)
(2)
 (3)
(3)
Разрешим систему уравнений (2) относительно неотрицательного базиса. Пусть система (2) при этом примет вид

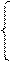
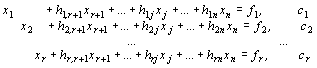 (4)
(4)
Получено опорное решение 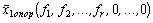 .
.
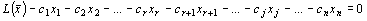 . (5)
. (5)
Исключим базисные переменные х 1, х 2, …, хr из целевой функции, для этого умножим первое уравнение системы (4) на с 1, второе на с 2 и т.д., r -е уравнение умножим на сr и все это прибавим к целевой функции. Получим:
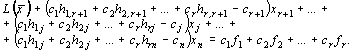 (6)
(6)
Определение 1. Выражение (6) называется приведенным выражением для целевой функции, коэффициенты при свободных переменных хr+ 1, …, хj, …, хn называются оценками и обозначаются D.
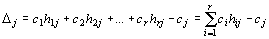 . (7)
. (7)
Правая часть уравнения (6)
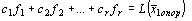 ,
,
так как 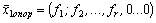 .
.
Тогда уравнение (6) примет вид
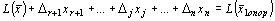 . (8)
. (8)
Запишем систему (5) и выражение (8) в виде одной системы и перейдем ко второму опорному решению:
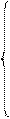
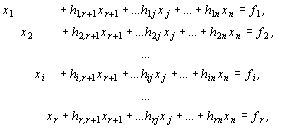 (9)
(9)
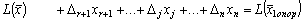 .
.
Допустим, что вместо xi в базис вводится свободная переменная xj. По правилу прямоугольника найдем значение целевой функции от второго опорного решения.
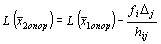 (10)
(10)
Сравним 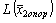 и
и 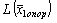 , так как fi ³0, hij > 0, то знак дроби
, так как fi ³0, hij > 0, то знак дроби 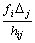 зависит от знака оценки Dj.
зависит от знака оценки Dj.
1) Если D j > 0, то 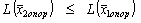 .
.
2) Если D j < 0, то 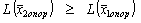 .
.
3) Если D j = 0, то 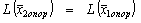 .
.
Отсюда получаем критерий оптимальности для ЗЛП на максимум:
1) если все оценки D j > 0, то найденное решение оптимальное;
2) если среди оценок имеется хотя бы одно отрицательное число, то найденное решение не оптимально.
Пусть Dj < 0, тогда если среди коэффициентов при хj есть хотя бы одно положительное число, хj можно ввести в базис и 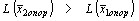 .
.
Если D j < 0 и все коэффициенты при хj hij < 0, то хj в базис ввести нельзя. Покажем, что 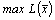 в этом случае равен бесконечности, для этого из системы (9) выпишем общее решение, всем свободным переменным, кроме хj, придадим значение, равное 0, получим
в этом случае равен бесконечности, для этого из системы (9) выпишем общее решение, всем свободным переменным, кроме хj, придадим значение, равное 0, получим
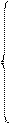
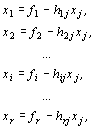 (11)
(11)
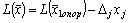 . (12)
. (12)
Отсюда видно, что если хj придавать сколь угодно большие числовые значения, то решение, полученное из системы (11), будет допустимым, а значение целевой функции (12) будет неограниченно расти, т.е. при х → ∞ 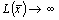 ;
;
3) предположим, что найдено оптимальное решение задачи, т.е. все оценки неотрицательны, и хотя бы одна из оценок свободных переменных равна нулю. Это говорит о наличии в задаче альтернативного оптимума. Если ввести в базис свободную переменную с нулевой оценкой, то получим второе опорное оптимальное решение, а значение целевой функции при этом не изменится.
Если нулевых оценок свободных переменных окажется несколько, то введение в базис каждой из этих переменных приводит к получению различных опорных оптимальных решений. Тогда задача имеет множество оптимальных решений, каждое из которых является выпуклой линейной комбинацией опорных оптимальных решений.
Алгоритм симплексного метода
Решение задач линейного программирования симплексным методом предполагает следующие этапы:
1) привести задачу к каноническому виду;
2) найти неотрицательное базисное решение системы ограничений;
3) найти оценки свободных переменных по формуле
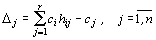
и записать полученные оценки в симплексную таблицу;
проверить найденное опорное решение на оптимальность: если требуется найти максимум целевой функции, то:
а) если все оценки Dj > 0, то найденное решение оптимально и задача решена;
б) если хотя бы одна оценка Dj < 0, а при соответствующей переменной х j нет ни одного положительного коэффициента, то задача не имеет оптимального решения из-за неограниченности целевой функции;
в) если хотя бы одна оценка Dj < 0, а при соответствующей переменной х j есть хотя бы один положительный коэффициент, то найденное решение не оптимально и его можно улучшить. Если отрицательных оценок несколько, то в базис вводят переменную с наибольшей по абсолютной величине отрицательной оценкой;
4) если выполняется случай в), то нужно перейти к следующему опорному решению;
5) перейти к п. 3.
Замечание 1. Критерием оптимальности для ЗЛП на минимум является неположительность оценок, т.е. все D j < 0, 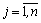 .
.
Замечание 2. В ЗЛП максимум и минимум целевой функции понимаются как глобальные.
Пример 3. Найти наибольшее значение функции
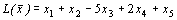
при ограничениях:
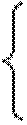
х 1-2х2 - 2х3 + х 4 - х 5 = 1,
-2 х 2 - х 3 +3х4 + х 5 = 5,
х2 + 8 х 3+ х 4 +3 х 5 = 20,
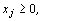
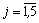 .
.
Задача задана в каноническом виде. Найдем исходное опорное решение.
| № п/п | Б.п. | х 1 | х 2 | х 3 | х 4 | х 5 | b i |
| x 1 | -2 -2 1 | -2 -1 | -1 | ||||
| x 1 x 2 | 8 | ||||||
| x 1 x 5 x 2 | 37/8 15/8 19/8 | -1/8 5/8 -7/8 | 103/8 45/8 25/8 |
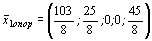 .
.
Проверим это решение на оптимальность.
| № п/п | сj | Б.п. | -5 | bi | ||||
| х 1 | х 2 | х 3 | х 4 | х 5 | ||||
| x 1 x 5 x 2 | 37/8 15/8 19/8 | -1/8 5/8 -7/8 | 103/8 45/8 25/8 | |||||
| D j | 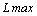 | 111/8 | -19/8 | 173/8 |
Найденное решение не оптимально, так как D4 < 0. Введем в базис свободную переменную с отрицательной оценкой х 4.
| № п/п | сj | Б.п. | -5 | bi | ||||
| х 1 | х 2 | х 3 | х 4 | х 5 | ||||
| x 1 x 4 x 2 | 1/5 8/5 7/5 | |||||||
| D j | 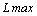 | 19/5 |
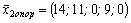 . Так как среди оценок нет отрицательных чисел, то второе опорное решение оптимально.
. Так как среди оценок нет отрицательных чисел, то второе опорное решение оптимально.
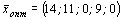 ,
, 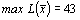 .
.
Метод искусственного базиса
При решении задач линейного программирования симплексным методом необходимо систему ограничений привести к единичному неотрицательному базису. Метод искусственного базиса дает возможность решать задачи без предварительного нахождения опорного решения.
Дана задача: найти наибольшее значение функции
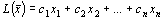
при ограничениях:
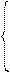
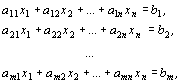
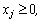
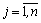 .
.
Составим расширенную задачу, которую назовем М-задачей.
Найти наибольшее значение функции
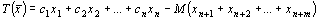
при ограничениях:
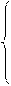
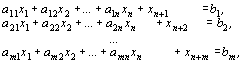
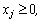
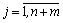 .
.
В каждое уравнение, в котором нет базисной переменной, вводим переменную 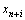 , где
, где 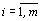 , с коэффициентом 1, эти переменные называются искусственными, и они образуют искусственный базис. Искусственные переменные вводятся в целевую функцию с коэффициентами -М, если задача решается на максимум, и +М, если задача решается на минимум, где М сколь угодно большое положительное число. Система ограничений расширенной задачи совместна.
, с коэффициентом 1, эти переменные называются искусственными, и они образуют искусственный базис. Искусственные переменные вводятся в целевую функцию с коэффициентами -М, если задача решается на максимум, и +М, если задача решается на минимум, где М сколь угодно большое положительное число. Система ограничений расширенной задачи совместна.
Исходное опорное решение 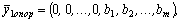 где
где 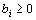 ,
, 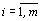 .
.
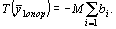
Между допустимыми решениями исходной и М-задачи есть связь. Если 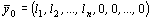 - допустимое решение М-задачи, то
- допустимое решение М-задачи, то 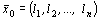 - допустимое решение исходной задачи, причем
- допустимое решение исходной задачи, причем
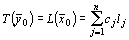 .
.
Эти решения называются соответствующими.
 2015-04-01
2015-04-01 988
988








