Предприятие может выпускать определенные виды продукции, используя для этого различные виды ресурсов. Известны затраты каждого вида ресурса на производство единицы каждого вида продукции и прибыль от реализации единицы каждого вида продукции. Требуется составить план выпуска продукции, чтобы при данных запасах ресурсов получить максимальную прибыль.
Составим математическую модель данной задачи.
Введем обозначения:
i - номер i -го вида ресурса, 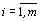 ;
;
bi - запасы i -го вида ресурса, 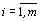 ;
;
j - номер j -го вида продукции, 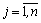 ;
;
aij - затраты i -го вида ресурса на производство единицы j -го вида продукции;
cj - прибыль от реализации единицы j -го вида продукции.
Все данные занесем в таблицу:
| Виды продукции Виды ресурсов | 1 2 … j … n | Запасы ресурсов |
| … i … m | a 11 a 12 … a 1 j … a 1 n a 21 a 22 … a 2 j … a 2 n … a i1 a i2 … aij … ain … am 1 am 2 … amj … amn | b 1 b 2 … bi … bm |
| Прибыль от реализации единицы продукции | c 1 c 2 … cj … cn |
Обозначим через xj - планируемый выпуск j -го вида продукции; 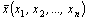 - план выпуска продукции. Тогда прибыль от реализации всей выпускаемой продукции составит
- план выпуска продукции. Тогда прибыль от реализации всей выпускаемой продукции составит
c 1 x 1 + c 2 x 2 +…+ cjxj +…+ cnxn.
Составим ограничения по ресурсам. Найдем расход первого вида ресурса:
a 11 x 1+ a 12 x 2+…+ a 1 jхj +…+ a 1 nxn.
Первый вид ресурса имеется в наличии b 1 условных единиц, т.е. получаем ограничение a 11 x 1+ a 12 x 2+…+ a 1 jxj +…+ a 1 nxn £ b 1.
Аналогично составляем ограничения по всем остальным видам ресурсов.
Кроме того, xj ³ 0, 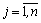 , так как количество продукции не может быть отрицательным числом.
, так как количество продукции не может быть отрицательным числом.
Получим ЗЛП: найти наибольшее значение функции 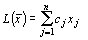 при ограничениях:
при ограничениях:
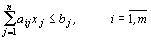 ,
,

Таким образом, математической моделью данной задачи является ЗЛП.
 2015-04-01
2015-04-01 763
763








