2015-04-01
1595
Запишем выражение для проекции ускорения жидкой частицы на какую-либо координатную ось, например, x. Имеем
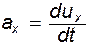
Для нахождения этой величины следует учесть, что проекция скорости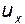 
(как и две другие проекции) является функцией координат x, y, z, которые, в свою очередь, в общем случае зависят от времени t. Представим величину 
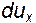в виде полного дифференциала
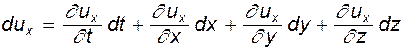
Разделим обе части на dt. Имея в виду, что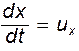 
, 
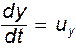и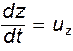 
, получим
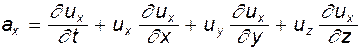(4.12)
Аналогичные соотношения можно записать и для двух других компонент.
Выражение (4.12) носит название полной либо субстанциональной производной. Установим смысл величин, входящих в нее. Производная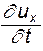 
- проекция локального ускорения, которое характеризует изменение скорости во времени в данной точке пространства. Локальное ускорение обусловлено нестационарностью процесса. Из чего следует, что если движение стационарное (установившееся), то локальное ускорение отсутствует, т.е. 
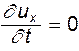. Три остальных члена (4.12) - проекции конвективного ускорения, которое возникает при переходе частицы от одной точки пространства к другой, оно обусловлено неравномерностью скоростного поля, т.е. неравномерным распределением скоростей.
