 |
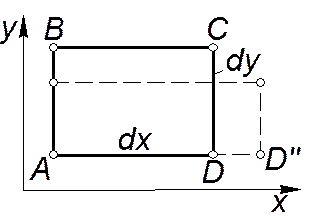
Очевидно, что линейные деформации частицы (рис. 4.8) могут возникнуть в результате различия в скоростях, совпадающих с направлением ребер. Как и ранее, компоненты скорости в точке A - 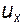 ,
, 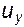 ,
, 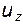 .
.
Вдоль оси x:
Точка A: 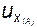
| Рис. 4.8 |
Точка D: 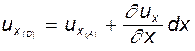
Разность скоростей, вызывающая удлинение ребра AD: 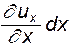 . Удлинение частицы
. Удлинение частицы 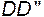 за время dt
за время dt
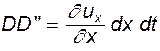 (4.28)
(4.28)
Относительное удлинение
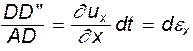 (4.29)
(4.29)
Скорость относительного удлинения
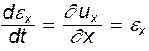 (4.30)
(4.30)
Аналогично для других осей
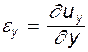 ;
; 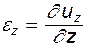
Если процесс происходит одновременно вдоль всех осей, то это приводит к объемному расширению либо сжатию частицы. Таким образом, объемная деформация сводится к изменению первоначального объема параллелепипеда 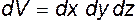 на величину
на величину 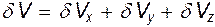 за счет растяжения либо сжатия ребер. При этом
за счет растяжения либо сжатия ребер. При этом 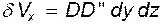 , и с учетом (4.28)
, и с учетом (4.28) 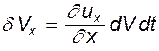 . Аналогично
. Аналогично 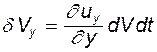 и
и 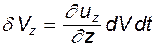 . Таким образом
. Таким образом
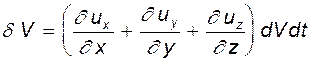
Скоростью относительной объемной деформации назовем отношение изменения объема к его первоначальному объему и скорости деформации, т.е.
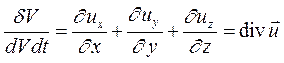 .
.
Если 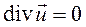 , то это означает, что
, то это означает, что 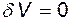 , т.е. деформация жидкой частицы происходит без изменения ее объема. В этом и заключается гидромеханический смысл равенства нулю дивергенции.
, т.е. деформация жидкой частицы происходит без изменения ее объема. В этом и заключается гидромеханический смысл равенства нулю дивергенции.
Полученную выше связь между поступательной и вращательной скоростями жидкой частицы можно получить и более коротким путем, представляющим определенный интерес. Разные подходы к одному и тому же вопросу способствуют углубленному пониманию. Поэтому рассмотрим этот путь.
 |
Пусть жидкая частица вращается вокруг оси z с угловой скоростью 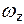 . Запишем выражение для ротора в проекциях на оси координат (см. формулу 1.8). Имеем:
. Запишем выражение для ротора в проекциях на оси координат (см. формулу 1.8). Имеем:
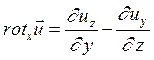
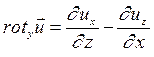
| Рис. 4.9 |
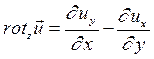
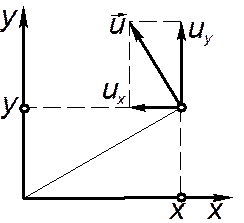 |
Рассмотрим точку M на жидкой частице (рис. 4.10).
Линейная скорость этой частицы 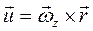 . Запишем выражения для проекций скоростей на оси координат:
. Запишем выражения для проекций скоростей на оси координат:
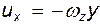 ;
;
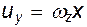 ;
;
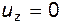
Откуда находим 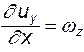 ;
; 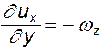 .
.
| Рис. 4.10 |
Таким образом
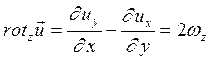
Аналогично для двух других компонент
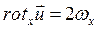 ;
; 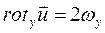
Либо в векторной форме
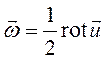
что полностью совпадает с (4.26).
Движение, при котором 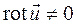 называют вихревым, при
называют вихревым, при 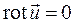 - безвихревым либо потенциальным. Из чего следует, что если течение вихревое, то движение жидких частиц происходит с вращением.
- безвихревым либо потенциальным. Из чего следует, что если течение вихревое, то движение жидких частиц происходит с вращением.
 2015-04-01
2015-04-01 1213
1213
