Циркуляция скорости

Для введения понятия о циркуляции скорости в настоящем пособии используется методика Н.Я.Фабриканта, приведенная в упомянутой выше книге. Несомненным преимуществом ее является то, что в отличие от других она позволяет ввести понятие циркуляции не чисто математически, а исходя из достаточно простых и ясных физических предпосылок.

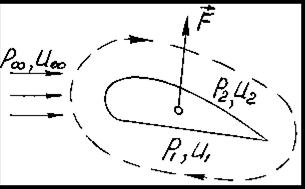Рассмотрим крыловой профиль, находящийся в потоке газа (воздуха). Как известно, на профиль в этом случае будет действовать подъемная сила (см. рис. 5.3). Физически наличие этой силы можно объяснить лишь тем, что давление под профилем (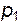) больше, а давление над профилем (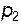) меньше, чем давление на каком-то удалении от него, которое мы обозначим 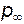. Это позволяет утверждать, что под крыловым профилем скорость 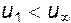, а над ним 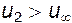. В данном случае 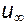- скорость невозмущенного потока.

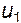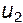Вычтем теперь из скоростей и скорость 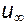, т.е. 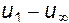и 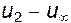. Это действие приводит нас к понятию потока возмущения, т.е. движения, которое возникает в среде из-за того, что в нее внесено инородное тело, т.е., по существу, это реакция потока, обусловленная в рассматриваемом случае тем, что в ней появился крыловой профиль. Установим теперь направление потоков возмущения. Под профилем 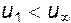, и он направлен против скорости 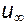, над профилем - наоборот. В результате появляется циркуляционный поток, направленный по часовой стрелке, как это показано на рис. 5.3. Теперь необходимо охарактеризовать этот поток количественно. Именно с этой целью вводится понятие циркуляции скорости по замкнутому контуру.

Рассмотрим замкнутый контур C, показанный на рис. 5.4. Пусть в произвольной точке M скорость равна 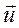. Составим скалярное произведени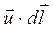е , где 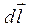- направленный элемент дуги.

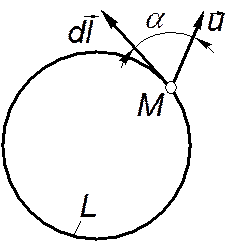Циркуляцией скорости называют контурный интеграл вида

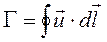(5.11)

Обратим внимание на структуру этого соотношения. Оно построено аналогично выражению для работы, поэтому иногда говорят, что циркуляция - это своеобраз­ная «работа» вектора скорости. Имея в виду, что 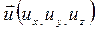и 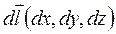, по правилу скалярного произведения получим

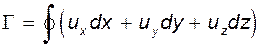(5.12)

Для плоского течения:

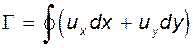(5.13)

В конце предыдущего раздела утверждалось, что понятие циркуляции является более удобным, чем интенсивность вихря. Действительно, из (5.13) следует, что для определения циркуляции достаточно знать проекции скорости, нахождение которых не связано с существенными трудностями. Однако остается пока открытым вопрос о том, существует ли связь между циркуляцией и интенсивностью вихря. Ответ на него дает теорема Стокса.