Гипотеза линейности

Применим закон Ньютона к жидкости, движущейся параллельно плоскости xOy (рис. 8.1), что дает

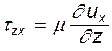
Воспользуемся результатом, полученным при рассмотрении теоремы Гельмгольца о движении жидкой частицы. Согласно теореме, скорость угловой деформации относительно оси y

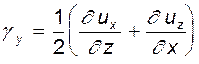
Так как движение происходит в плоскости xOy, то 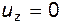и

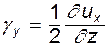
и, следовательно, касательное напряжение

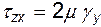(8.1)

Полученный результат иллюстрирует так называемый закон трения Стокса. Согласно этому закону, напряжения, возникающие в жидкости, в отличие от твердого тела, пропорциональны не величинам, а скоростям деформаций, и связаны с ними линейной зависимостью. При этом коэффициент пропорциональности остается неизменным и равным 2.

Кроме того, согласно закону Стокса касательные напряжения, как показано выше, пропорциональны скоростям угловой деформации, а нормальные - скорости линейной деформации, т.е. , , .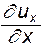

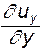Таким образом, можем записать

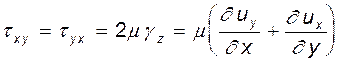(8.2)

и т.д.

Рассмотрим теперь нормальные напряжения, возникающие от сил вязкости. Согласно закону Стокса, их можно записать в виде так называемых девиаторов напряжения, имеющих вид:

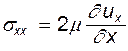
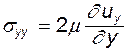(8.3)

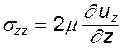
Полные нормальные напряжения отличаются тем, что помимо записанных выше в любой, как в вязкой, так и в невязкой жидкости, действуют и статические давления. Другими словами

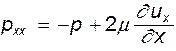
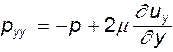(8.4)

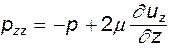
Выполним следующую операцию: из утроенной величины 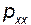вычтем сумму (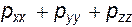). Это дает:

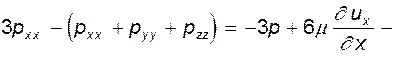
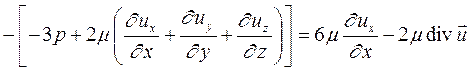
откуда найдем

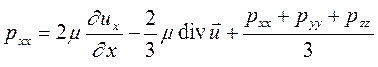
В качестве давления в вязкой жидкости принимают среднее арифметическое, т.е. 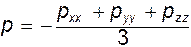. И, следовательно,

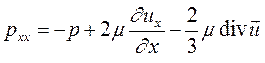
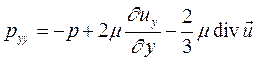(8.5)

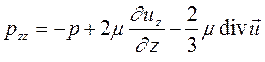
Для несжимаемой жидкости 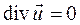, и выражения упрощаются.