2015-04-01
618
В качестве численного метода нелинейного программирования второго порядка рассмотрим метод Ньютона для задачи
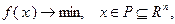(3.5.45)
где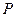 
– выпуклое замкнутое множество, функция 
дважды непрерывно дифференцируема на 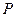. Пусть 
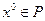– некоторое начальное приближение. Если известно 
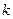-е приближение 
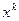, то приращение функции в точке 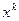можно представить в виде
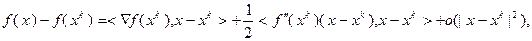
где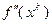 
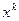– матрица вторых производных (матрица Гессе) функции , вычисленных в точке . Возьмем квадратичную часть этого приращения
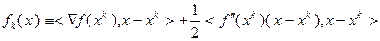(3.5.46)
и определим вспомогательное приближение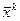 
из условий
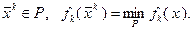(3.5.47)
Следующее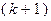 
-е приближение будем искать в виде
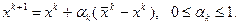(3.5.48)
В зависимости от способа выбора величины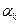 
в (3.5.48) можно получить различные варианты метода (3.5.46) – (3.5.48), называемого методом Ньютона.
Если в (3.5.48) принять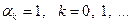 
, то в этом случае, как следует из (3.5.48), 
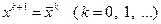, т.е. условие (3.5.47) сразу определяет следующее 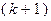-е приближение. Иначе говоря,
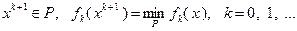(3.5.49)
В частности, когда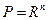 
, в точке минимума функции 
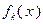ее производная 
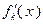обращается в нуль, т.е.
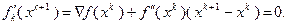(3.5.50)
Это значит, что на каждой итерации метода (3.5.46) – (3.5.49) нужно решать линейную систему алгебраических уравнений (3.5.50) относительно неизвестной разности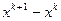 
. Если матрица этой системы 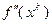– невырожденная, то из (3.5.50) получим
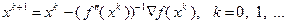
Метод Ньютона для решения задачи (3.5.45) обычно применяют в тех случаях, когда вычисление производных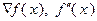 
не представляет особых трудностей и вспомогательная задача (3.5.47) решается достаточно просто. Достоинством метода Ньютона является высокая скорость сходимости.
