Метода потенциалов

1.Находится первый опорный план по одному из рассмотренных методов.

2.Проверяется найденный опорный план на оптимальность:

2.1. Находятся потенциалы поставщиков и потребителей по формуле (3.67).

Примечание. Т. к. в опорном плане заполнено m+n-1 клеток таблицы транспортной задачи, то для нахождения потенциалов по данному плану можно составить систему из m+n-1 линейно независимых уравнений с m+n неизвестными. Такая система является неопределенной, и поэтому одной неизвестной (обычно 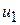) придают нулевое значение, а остальные находятся однозначно по формуле (3.67).

2.2. Проверяется, выполнено ли условие (3.68) или, что то же самое, услови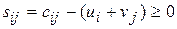е , где 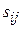- характеристика каждой свободной клетки таблицы. Если для всех свободных клеток таблицы условие (3.68) выполнено, т.е.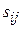 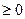, то опорный план транспортной задачи является оптимальным (решение задачи завершено). Если для некоторых свободных клеток таблицы 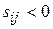, то клетка с наименьшим значением 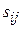является перспективной, и выполняется следующий этап алгоритма.

2.3. К перспективной клетке строится цикл, расставляются знаки по циклу, при этом в перспективную клетку ставится плюс, а остальные знаки в вершинах цикла чередуются, и определяется величина перераспределения груза по формул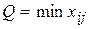е , где 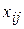- объем перевозки груза, записанный в клетках (вершинах) цикла таблицы, отмеченных знаком минус.

2.4. Осуществляется перераспределение груза по циклу на величину Q. В результате будет получен новый опорный план, который проверяется на оптимальность, т.е. производится переход к пункту 2.1 алгоритма.

Пример 3.23. Три завода производят однородную продукцию в количестве 650, 850 и 700 единиц соответственно. Эта продукция требуется четырем потребителям в количестве 500, 800, 300 и 600 единиц каждому. Требуется спланировать перевозку груза так, чтобы суммарные транспортные затраты были минимальными.

Затраты на перевозку единицы продукции (тыс. руб.) от каждого завода к каждому потребителю заданы матрицей:

.

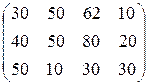Решение. Занесем данные транспортной задачи в таблицу 3.36 и найдем опорный план перевозок продукции методом минимальной стоимости.

Таблица 3.36. Первый опорный план для примера 3.23

Поставщики	Потребители	Объем производства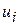
1	2	3	4
1
2		+	-
3		-	+			-30
Спрос

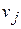
Найденный план является невырожденным, т.к. в таблице заполнено ровно 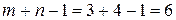клеток. Затраты на перевозку продукции для данного плана равны:

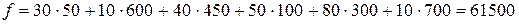(т.р.).

Находим потенциалы поставщиков и потребителей. Составляем систему:

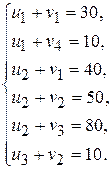
Полагая 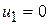, находим все другие потенциалы.

Найдем характеристики свободных клеток таблицы транспортной задачи по формуле .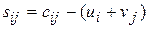

, ,

, ,

, .

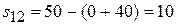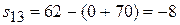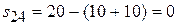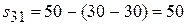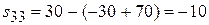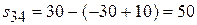Т.к. 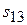<0 и 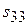<0, то план в таблице 3.36 неоптимальный, и перспективной клеткой будет клетка (3,3) с наименьшей характеристикой .

Строим цикл к перспективной клетке μ=[(3,3),(3,2),(2,2),(2,3),(3,3)] и находим величину груза Q=min (300,700)=300.

Осуществляем перераспределение груза по циклу, добавляя величину Q =300 в клетках со знаком «+» и вычитая – в клетках со знаком «–». В результате получаем новый опорный план (таблица 3.37).

Таблица 3.37. Второй опорный план для примера 3.23

Поставщики	Потребители	Объем производства
1	2	3	4
1
2
3						-30
Спрос

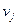
Применяя далее алгоритм решения задачи, находим потенциалы поставщиков и потребителей. Составляем систему:

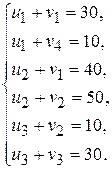
Полагая 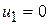, находим все другие потенциалы.

Найдем характеристики свободных клеток таблицы:

, ,

, ,

, .

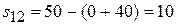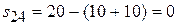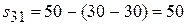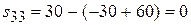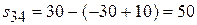Т.к. для всех свободных клеток 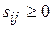, то данный опорный план является оптимальным. Суммарные минимальные затраты на перевозку продукции:

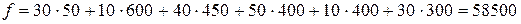(т.р.).

Эти минимальные затраты достигаются при следующих объемах перевозок:

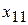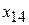=50, =60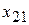0, =450,

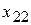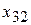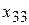=400, =400, =300.

Остальные неизвестные равны нулю.

Замечание. Многие экономические задачи (например, оптимальное закрепление за станками операций по обработке деталей, распределение сельскохозяйственных культур за посевными площадями участков земли) также сводится к решению транспортной задачи. Правда, как правило, в этих случаях необходимо находить максимум функции (количество обработанных деталей, суммарный сбор зерна должны быть как можно большими).

Для решения задач транспортного типа на максимум необходимо коэффициенты 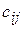при неизвестных в целевой функции взять со знаком минус, т.е. необходимо перейти к нахождению минимума измененной функции.