Рассмотрим теорему об оптимальности решения транспортной задачи (3.61)-(3.64).
Теорема 3.10. Решение транспортной задачи будет оптимальным, если найдутся такие числа 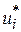 (i =1,2,…, m) и
(i =1,2,…, m) и 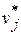 (j =1,2,…, n), называемые соответственно потенциалами поставщиков и потребителей,которые будут удовлетворять условиям:
(j =1,2,…, n), называемые соответственно потенциалами поставщиков и потребителей,которые будут удовлетворять условиям:
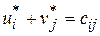 для
для 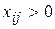 ;
;
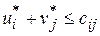 для
для 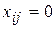 ,
,
i= 1,2,…, m; j= 1,2,…, n.
По общему правилу построения двойственных задач запишем двойственную задачу к задаче (3.61)-(3.64), для чего введем обозначения двойственных оценок:
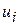 (i= 1,2,…, m) – оценка единицы запаса (потенциал поставщика),
(i= 1,2,…, m) – оценка единицы запаса (потенциал поставщика),
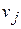 (j= 1,2,…, n) – оценка единицы спроса (потенциал потребителя).
(j= 1,2,…, n) – оценка единицы спроса (потенциал потребителя).
Тогда двойственная задача запишется так:
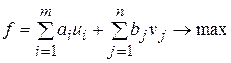 (3.65)
(3.65)
при ограничениях
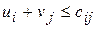 , (3.66)
, (3.66)
причем 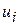 (i =2,3,…, m) и
(i =2,3,…, m) и 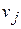 (j= 1,2,…, n) – произвольного знака.
(j= 1,2,…, n) – произвольного знака.
Т.к. задача (3.61)-(3.64) имеет решение, то по основной теореме двойственности, и двойственная к ней задача также имеет решение, при этом 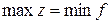 .
.
На основании 5-го правила построения двойственных задач, устанавливающим взаимосвязь между значениями неизвестных и выполнением ограничений в оптимальных решениях взаимно двойственных задач, заключаем, что ограничения двойственной задачи из системы ограничений (3.66) выполняются как строгие равенства, если им в исходной задаче соответствуют положительные неизвестные 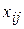 ; а ограничения, соответствующие неизвестным
; а ограничения, соответствующие неизвестным 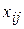 =0, выполняются как неравенства. Таким образом,
=0, выполняются как неравенства. Таким образом,
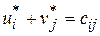 для
для 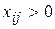 ; (3.67)
; (3.67)
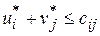 для
для 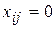 . (3.68)
. (3.68)
Теорема доказана.
 2015-04-01
2015-04-01 357
357








