В таблице из всех значений стоимостей выбираем наименьшее и в клетку (i, j) с наименьшей стоимостью записываем меньшее из чисел 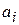 и
и 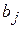 . Исключаем из рассмотрения строку i, если запас
. Исключаем из рассмотрения строку i, если запас 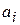 вывезен полностью; или столбец j, если спрос
вывезен полностью; или столбец j, если спрос 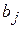 удовлетворен полностью; или и строку и столбец, если
удовлетворен полностью; или и строку и столбец, если 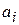 =
= 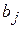 . Среди остальных стоимостей снова выбираем наименьшую и заполняем соответствующую клетку таблицы. Таким же образом продолжаем заполнять клетки таблицы, пока не будет найдено опорное решение.
. Среди остальных стоимостей снова выбираем наименьшую и заполняем соответствующую клетку таблицы. Таким же образом продолжаем заполнять клетки таблицы, пока не будет найдено опорное решение.
Пример 3.21. Рассмотрим метод на примере, исходные данные которого представлены в таблице 3.33:
Таблица 3.33. Исходные данные для примера 3.21
| Поставщики | Потребители | Запас | |||
| 1 | 2 | 3 | 4 | ||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| Спрос |
Полученное в таблице решение неопорное, т.к. заполнено 5 клеток, а требуется 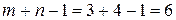 . занесем в клетку (1,3) объем перевозки, равный нулю. В результате получено ацикличное, вырожденное опорное решение. Заметим, что нулевой объем перевозки можно было разместить в любой свободной клетке таблицы, за исключением клеток (2,3) и (3,2). Если нуль поместить в одну из этих клеток, то клетка с нулем с другими заполненными клетками образует цикл, что недопустимо.
. занесем в клетку (1,3) объем перевозки, равный нулю. В результате получено ацикличное, вырожденное опорное решение. Заметим, что нулевой объем перевозки можно было разместить в любой свободной клетке таблицы, за исключением клеток (2,3) и (3,2). Если нуль поместить в одну из этих клеток, то клетка с нулем с другими заполненными клетками образует цикл, что недопустимо.
Суммарные затраты на перевозку грузов равны:
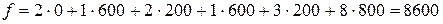 .
.
 2015-04-01
2015-04-01 328
328








