Реактивная и комплексная обратная связь

Реактивная обратная связь устанавливается при условии 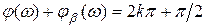, т.е. при поступлении на вход основной цепи сигнала

обратной связи с фазовым сдвигом относительно входного сигнала, равным 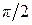. В этом случае 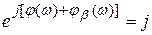и модуль коэффициента передачи равен

.

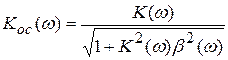В данном случае отрицательная обратная связь также может уменьшать энергию входного воздействия основной цепи, что приводит к уменьшению модуля коэффициента передачи цепи с обратной связью.

При остальных значениях суммарного фазового сдвига 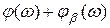обратная связь будет комплексной.

В общем случае величина суммарного фазового сдвига в цепи с обратной связью зависит от частоты. Поэтому характер обратной связи также во многом определяется рабочим частотным диапазоном цепи.

Таким образом, частотные свойства цепи с обратной связью зависит от 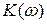и 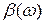. При необходимости изменить какие-либо характеристики основной цепи с коэффициентом передачи 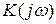, можно, не изменяя структуры и параметров этой цепи, ввести обратную связь с соответствующим коэффициентом 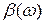и получить требуемые характеристики цепи в целом.

Рассмотрим целесообразность использования обратной связи.

5.7.2. Стабилизация коэффициента усиления

Определим относительную нестабильность коэффициента передачи цепи с обратной связью.

Полагаем, что рассматриваемая цепь представляет собой усилитель, охваченный отрицательной обратной связью. Коэффициент усиления усилителя и коэффициент передачи цепи обратной связи в определенном диапазоне частот являются действительными величинами, т.е. 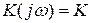и 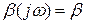. Для оценки нестабильности коэффициента усиления определим значение параметра, определяемого выражением 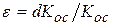и характеризующего относительное изменение коэффициента передачи цепи с обратной связью.

;

.

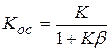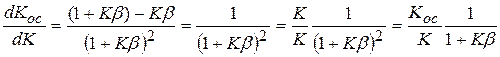Тогда .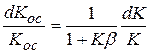

Таким образом, относительное изменение коэффициента усиления усилителя, охваченного обратной связью, может сильно отличаться от относительного изменения коэффициента усиления при отсутствии обратной связи. При этом если обратная связь отрицательная, то относительная нестабильность коэффициента усиления уменьшается. Например, при 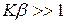относительная нестабильность падает в 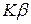раз. В данном случае коэффициент усиления цепи с обратной связью определяется только значением 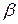, т.е. не зависит от нестабильности коэффициента усиления усилителя без ОС.

5.7.3. Коррекция амплитудно-частотной характеристики

Применение отрицательной обратной связи позволяет уменьшить относительное изменение частотного коэффициента передачи, т.е. реализовать "выравнивание" АЧХ.

Рассмотрим резонансный усилитель с частотным коэффициентом передачи

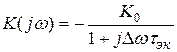
Охватив этот усилитель цепью частотно-независимой отрицательной обратной связи, получим

.

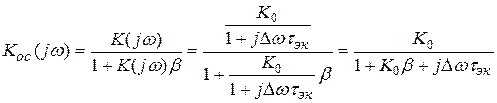Таким образом, АЧХ усилителя, охваченного отрицательной обратной связью, определяется выражением

.

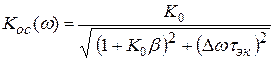На рис. 5.12 приведено семейство АЧХ с различными уровнями обратной связи, т.е. различными значениями 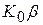. Из рисунка видно, что график АЧХ цепи с обратной связью значительно ровнее, чем график АЧХ цепи без обратной связи. Выравнивание АЧХ цепи с обратной связью сопровождается снижением графика 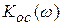, т.е. уменьшением коэффициента усиления, что является результатом действия отрицательной обратной связи.

5.7.4. Подавление нелинейных искажений

Нелинейность характеристик элементов цепи приводит к возникновению высших (паразитных) гармоник в спектре преобразуемого сигнала, что является причиной нелинейных искажений. Внутренние шумы активных цепей, особенно шумы выходного каскада в многокаскадном усилителе, представляющем собой последовательное соединение одиночных усилительных каскадов, также могут привести к искажениям выходных сигналов. Оценим влияние обратной связи на величину этих искажений.

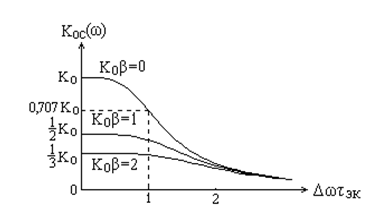
Рис. 5.12. Влияние обратной связи на АЧХ

Предположим, что паразитный сигнал, соответствующий нежелательным высшим гармоникам, появляется внутри активного элемента. Место его появления делит активный элемент на две каскадно включенные части с коэффициентами передач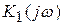и и 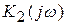(рис. 5.13).

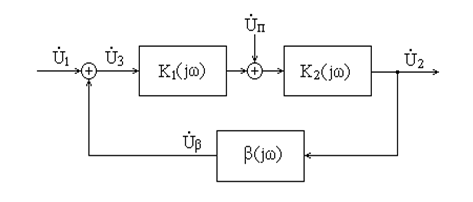
Рис. 5.13. Подавление паразитного сигнала с помощью цепи обратной связи

Введем отрицательную обратную связь. Тогда для паразитного сигнала частотный коэффициент передачи будет иметь вид

.

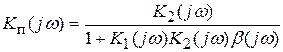Следовательно, паразитный сигнал (нежелательные гармонические составляющие или шумы) на выходе цепи с отрицательной обратной связью будет в 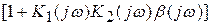раз меньше, чем в случае отсутствия обратной связи. Ослабление паразитного сигнала особенно существенно, если в пределах эффективной полосы пропускания 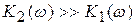. Заметим, что введение отрицательной обратной связи приводит к ослаблению и полезного сигнала. Однако его ослабление можно компенсировать предварительным или последующим усилением.

5.7.5. Устойчивость цепей с обратной связью

а. Понятие об устойчивости

Система устойчива, если выведенная из состояния равновесия, она в него возвращается. По существу в устойчивой системе при нулевом входном сигнале выходной сигнал затухает при любых начальных условиях, т.е.

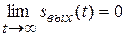при .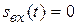

Применение обратной связи тесно связано с проблемой обеспечения устойчивости. Устойчивость может быть нарушена в силу наличия в структуре цепи реактивных элементов (паразитные емкости монтажа, индуктивности проводов, межэлектродные емкости транзисторов), способных накапливать энергию и создавать дополнительные фазовые сдвиги. Поэтому при проектировании и исследовании различных цепей большое значение имеют методы определения устойчивости цепи.

В настоящее время известно несколько критериев устойчивости, различающихся в основном по форме, а не по содержанию. В основе их лежит идея устойчивости решений однородного дифференциального уравнения, описывающего свободные (собственные) колебания цепи после исчезновения возмущающих сил, т.е.

.

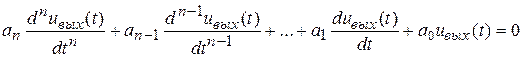Решение уравнения, как известно, имеет вид

,

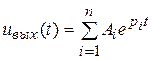где 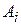– постоянные числа, определяемые из n начальных условий;

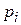– корни характеристического уравнения

, , , .

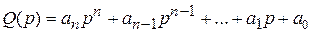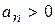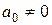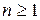Корни характеристического уравнения являются в общем случае комплексными числами, т.е. .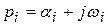

Для устойчивой цепи входящие в решение дифференциального уравнения экспоненты должны быть затухающими. Это значит, что корни характеристического уравнения должны быть либо отрицательными вещественными числами, либо комплексными числами с отрицательными действительными частями.

Таким образом, можно сформулировать следующий основной критерий устойчивости линейных цепей: линейная цепь устойчива, если действительные части всех корней характеристического уравнения отрицательны.

Пользоваться этим критерием для систем, описываемых дифференциальными уравнениями выше второго порядка, затруднительно. Поэтому были разработаны специальные критерии устойчивости, позволяющие судить об устойчивости любой цепи без решения характеристического уравнения.

б. Критерий устойчивости Гурвица

Критерий швейцарского математика А. Гурвица относится к алгебраическим критериям устойчивости. Он позволяет судить об устойчивости системы по результатам анализа соотношений между коэффициентами характеристического уравнения без определения его корней.

Формулировка критерия Гурвица.

Для того чтобы корни характеристического уравнения имели отрицательные действительные части, необходимо и достаточно, чтобы выполнялись неравенства , , , …, .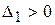

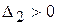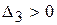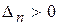Здесь 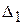, , 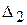,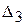… - последовательные определители, равные

; , ,...

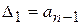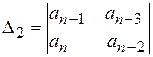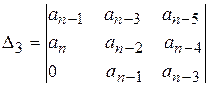Последовательные определители равны главным диагональным минорам матрицы Гурвица

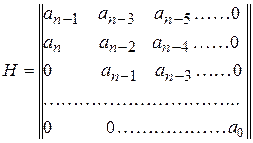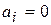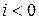, при и .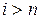

Последний столбец матрицы 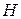содержит лишь один отличный от нуля элемент 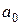, расположенный на главной диагонали. Поэтому 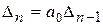. Следовательно, условия устойчивости можно записать в виде таких неравенств , , , …, , .

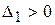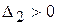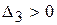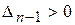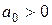Данный критерий позволяет проверить устойчивость системы при заданных параметрах (коэффициентах дифференциального уравнения). В то же время им невозможно пользоваться при экспериментальных исследованиях, когда известны только частотные характеристики прямой и обратной цепей. Трудно также определить параметры, изменение которых приводит к устойчивости цепи.

Пример.

Резонансный усилитель с положительной ОС при определенных условиях может работать как автогенератор гармонических колебаний. На рис. 5.14 представлена схема такого автогенератора, называемого LC - генератором.

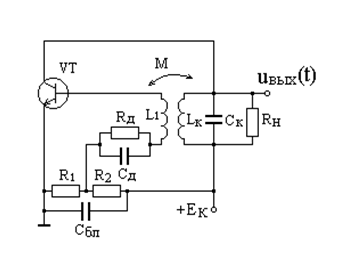
Рис. 5.14. Схема LC -генератора

Дифференциальное уравнение резонансного усилителя с трансформаторной положительной ОС имеет вид

.

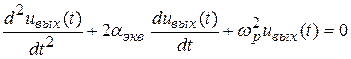Здесь

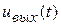– напряжение на выходе генератора;

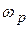– резонансная частота контура;

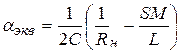– эквивалентный коэффициент затухания.

Запишем характеристическое уравнение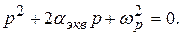

В соответствии с критерием Гурвица получаются следующие условия устойчивости:

.

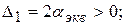
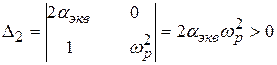Система будет устойчивой при следующих соотношениях между параметрами схемы:

.

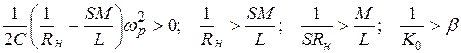Окончательно получим .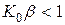

Таким образом, рассматриваемая система с положительной обратной связью устойчиво работает как усилитель, если коэффициент усиления разомкнутой цепи удовлетворяет условию 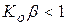. В свою очередь, при 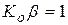система находится на границе устойчивости, а при 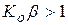– в неустойчивом состоянии, т.е. работает как генератор.

Последние условия являются условиями работы LC -генератора и называются "баланс амплитуд". При 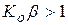генератор работает в переходном режиме (при включении питания), при 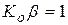– в стационарном режиме.

в. Критерий устойчивости Найквиста

Критерий американского ученого Найквиста относится к частотным критериям. Для анализа устойчивости используется частотный коэффициент передачи цепи с обратной связью

.

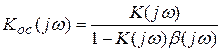Глубина и характер обратной связи определяется величиной .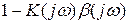

При 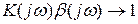цепь с обратной связью приближается к границе устойчивости. При 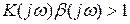цепь с положительной ОС работает в неустойчивом режиме (в режиме самовозбуждения). Поэтому в основу рассматриваемого критерия положен геометрический метод определения следующих услови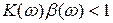й:

и .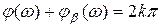

Для этого рассматривается коэффициент передачи цепи с разомкнутой обратной связью 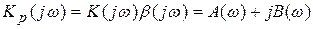и строится годограф 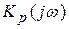как функция частоты 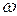на плоскости .

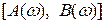Формулировка критерия Найквиста.

Система с обратной связью будет устойчивой, если годограф коэффициента передачи разомкнутой системы не охватывает точку (1, 0) на комплексной плоскости .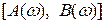

На рис. 5.15,а приведен годограф устойчивой системы, описываемой дифференциальным уравнением второго порядка, а на рис. 15.15,б – годограф неустойчивой системы.

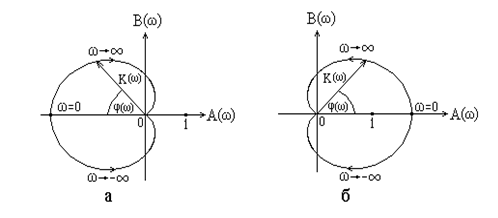
Рис. 5.15. Годографы устойчивой (а) и неустойчивой (б) цепей с ОС

г. Критерий устойчивости Михайлова

Критерий русского ученого Михайлова относится к аналитическим критериям. Для анализа устойчивости используется характеристическое уравнение цепи с обратной связью, т.е. уравнение вида

.

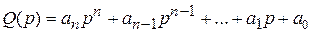Подставив в данное уравнени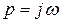е , где 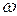– действительная переменная, получим

.

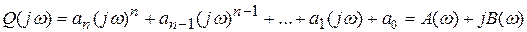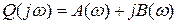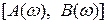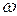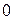Годограф функции , получающийся на комплексной плоскости при изменении частоты от до 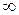, называется кривой (годографом) Михайлова.

Формулировка критерия Михайлова.

Для того чтобы система была устойчивой, необходимо и достаточно, чтобы годограф функции 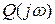при изменении 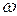от 0 до 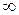последовательно прошел против часовой стрелки 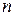квадрантов комплексной плоскости, начинаясь на действительной оси (при ).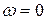

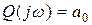На рис. 5.16,а приведены годографы устойчивых систем, описываемых дифференциальными уравнениями различного порядка, а на рис. 5.16,б – годографы неустойчивых систем.

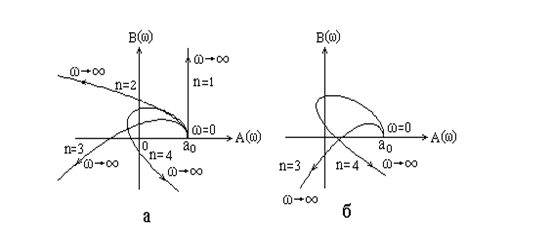
Рис. 5.16. Годографы устойчивых (а) и неустойчивых (б) систем

с обратной связью

Критерий Михайлова применяется в тех случаях, когда возникает необходимость оценить влияние изменений структуры и параметров системы на ее устойчивость.