Алгоритм ROCK (robust clustering using links)

Данный алгоритм построен на принципе соседства точек, который очень близок принципу и понятию взаимного соседства. Создатели ROCK вводят два основных понятия, уже использовавшиеся не раз в кластерном анализе: сосед и связь. Соседями объекта они называют объекты, которые в достаточной степени ему близки. В формализованном виде это выглядит так:

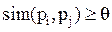, (40)

то есть две точки p_i и p_j считаются соседями, если значение их сходства превышает заданный порог q.

Далее, авторы данного алгоритма расширяют понятие связи (п. 0) и утверждают, что связей между двумя объектами может быть несколько. То есть, связей ровно столько, сколько общих соседей у двух объектов.

Значение функции связи 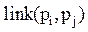между двумя точками p_i и p_j соответствует количеству общих соседей соответствующих точек. По определению, если у двух точек большое значение функции связи, то они, скорее всего, принадлежат одному кластеру. Кластеризация с использованием данного понятия связи делает сам процесс разбиения более глобальным, чувствительным к общей структуре, а не только к локальным характеристикам точек.

Таким образом, задача кластеризации сводиться к такому разбиению точек на кластеры, которое максимизирует сумму связей точек принадлежащих одному кластеру, и минимизирует эту функцию для точек из разных кластеров. Таким образом, можно получить следующую целевую функцию для некоторого желательного разбиения на k кластеров:

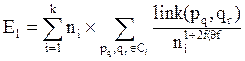, (41)

где C_i – кластер i размера n.

Данная функция отличается от простой суммы связей для каждого кластера, поскольку такая функция бы не давала уверенности в том, что точки, имеющие мало связей между собой распределялись бы по разным кластерам. Поэтому действительную сумму связей в кластере следует разделить на, так называемую, ожидаемую сумму связей – 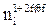(при том, что ожидаемая сумма соседей – ).

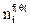Вид функции f выбирается пользователем и обычно используют 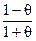.Такое взвешивание предупреждает отнесение точек с низкими значениями связи к одному кластеру, поскольку это будет увеличивать ожидаемое число связей для кластера и уменьшать целевую функцию. Значение связи между кластерами определяется как:

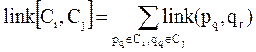, (42)

то есть как сумма попарных связей точек, принадлежащих разным кластерам.

Целевая функция качества, использующаяся при выборе кластеров для объединения:

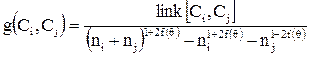. (43)

Та пара кластеров, для которой эта функция максимальна, наиболее подходит для объединения. Опять же, эта функция могла бы состоять только из значения связи кластеров, как в случае с точками это значение могло бы послужить оптимальным определением близости. Но на самом деле это не так. Такой подход мог бы привести к той же проблеме, что возникала и ранее – точки могли бы быть несправедливо отнесены к одному кластеру, поскольку больший кластер, как правило, обладает большим количеством связей с другими, чем меньший и может, в этом аспекте, притягивать мелкие, но суверенные кластеры. Поэтому значение связи между кластерами в этой функции делиться на ожидаемое значение связи:

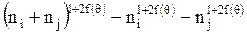. (44)

Теперь опишем подробнее сам алгоритм кластеризации.

На входе данного алгоритма некий набор n точек S. Кроме того, заданное значение k кластеров желаемого разбиения.

В начале каждая точка представляется отдельным кластером и для каждого из них вычисляется значение связи и значение функции качества объединения с каждым другим кластером. На каждом шаге объединяется пара с максимальным значением этой функции. После объединения необходимо пересчитать те же значения связи и качества для новообразованного кластера.

Процесс завершается после получения желаемого числа k кластеров.

Общая максимальная вычислительная сложность алгоритма равна 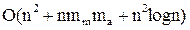, где m_m – максимальное количество возможных соседей, m_a – среднее число соседей и n – количество объектов.