Практически все методы, разобранные выше, основаны на операциях с матрицей сходства. Этот подход кажется наиболее перспективным для многомерных пространств еще и в свете наибольшей адекватности для иерархического кластерного анализа в таких пространствах метода объединения кластеров по принципу попарного среднего. Как было показано ранее, этот метод объединения опирается исключительно на сходство объектов в пространстве, не рассматривает их координаты, не использует понятие среднего вектора (центра тяжести) и, вообще, целиком опирается на графо-ориентированный подход, рассматривая полный граф, построенный на матрице сходства. Все четыре метода, рассмотренные в это работе, совершенствуют данный подход.
Так, ROCK на основе матрицы сходства конструирует граф, используя пороговое значение сходства и принцип общих соседей. По схожей схеме действует метод, основанный на значении взаимного соседства (mnv). CURE также неявно использует в своем алгоритме надстройку над матрицей сходства в виде специального графа, содержащего только представительные точки для каждого кластера. В этом графе присутствуют только ребра, соединяющие точки разных кластеров, после чего выбирается ребро с наибольшим весом, и кластеры, которые оно соединяет, объединяются. Алгоритм CHAMELEON при первоначальной обработке также строит граф по принципу k ближайших соседей и потом использует понятие связи на основе этого графа. Все эти методы безусловно имеют преимущества по сравнению с методами кластеризации, основанными на других мерах близости кластеров. Однако, и у них в той или иной степени встречаются серьезные недостатки.
|
|
|
Несмотря на то, что была доказана наибольшая перспективность агломеративных методов, использующих в той или иной степени принцип попарного среднего, следовало обратить внимание на алгоритм CURE, поскольку он решает проблемы остальных методов в определении различных форм и размеров кластеров, не используя этот принцип. Тем не менее, основанный только на сходстве отдельных точек в кластерах, он, очевидно, может давать положительные результаты, только в случае достаточно равномерного распределения объектов в пространстве, поскольку не учитывает плотности объединяемых кластеров. Так, на Рисунке 7 и 8 изображены по две группы объектов. Вторая пара – лучший кандидат в объединение, исходя из требования к однородности объектов в кластере, а первая, хоть и характеризуется большой взаимной близостью и может быть объединена, на данном этапе должна остаться без изменений.
Алгоритм CURE провел бы верное объединение, только если бы использовал параметр сокращения расстояния представительных точек от центра a=0, то есть объединял бы по методу ближайшего соседа. Однако, тогда исчезали бы его преимущества в определении формы кластеров. В остальных случаях, поскольку CURE не учитывает разницу в плотности (связности) и основан только на взаимном сходстве, данный алгоритм выбрал бы первое, неверное объединение. Если бы сравнивались пары кластеров на Рисунках 8 и 9, то опять же, CURE выбрал бы пару 9, что неверно, вследствие большей взаимной однородности, плотности пары на рисунке 8.
|
|
|

Рисунок 7 – Распределение объектов 1

Рисунок 8 – Распределение объектов 2
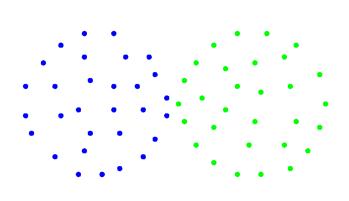
Рисунок 9 – Распределение объектов 3
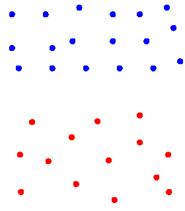
Рисунок 10 – Распределение объектов 4


Рисунок 11 – Распределение объектов 5
Алгоритм ROCK при выборе между парой 7 и парой 8, скорее отдаст предпочтение второй паре, поскольку, плотность создаваемых кластеров ведется с учетом размера кластеров (ожидаемого числа связей в новом кластере). Однако и в этой ситуации ROCK может дать сбой, когда число объектов будет одинаково, а плотность различна. Алгоритм ROCK основан на заданном пользователем пороге близости, то есть, фактически не может учитываться разница во внутренней плотности кластеров. Если распределение объектов в пространстве не равномерное, и плотности на разных его участках различны, алгоритм будет стремиться объединить наиболее плотные кластеры, потому что количество общих соседей для объектов из этих кластеров больше, чем в более разреженных кластерах. Также, ROCK в определенных ситуациях, таких как на рисунках 10 и 11, может совершить неверное объединение (выбрать пару 11), потому что, будучи основан на неверной модели связности (слишком большом пороге близости), не будет учитывать большую силу сходства отдельных объектов, а возьмет в рассмотрение лишь количество связей. Причем метод, основанный на простом попарном среднем в любом случае даст неверный результат.
Можно сделать вывод о том, что методы использующие только значения сходства отдельных точек при объединении кластеров не справляются с анализом кластеров различной плотности. Методы, использующие попарное среднее, хотя в целом и предпочтительнее, как уже было доказано, однако, могут некорректно распознавать кластеры разных форм и плотности, поскольку основаны только на локальном сходстве объектов.
Методы, использующие преобразованный метод попарного среднего, рассматривающие глобальное сходство точек (то есть, количество связей, соседей объекта), вместо локального, безусловно эффективнее предыдущих. Однако, как в алгоритме ROCK, задание связей на основе статического порогового значения сходства может привести к неверным объединениям, как было показано, вследствие неравномерной плотности кластеров расположенных на разных участках пространства.
Таким образом, наибольшую адекватность, очевидно, имеют методы, использующие как глобальное сходство всех объектов в сравниваемых кластерах, так и степень локального сходства. То есть, для оптимального определения необходимости объединения важно учесть следующие факторы.
Во-первых, количество общих соседей точек, что позволит ввести понятие связи и рассматривать только сходства превышающие некий порог (объекты, достаточно далекие друг от друга будут обладать нулевыми значениями связи, у них не будет общих соседей). Причем, как было доказано выделение соседей на основе заданного порогового значения сходства является неэффективным, поскольку может не учитывать различия в плотности кластеров. Такой порог можно устанавливать неявно для каждого объекта или кластера (при объединении), если использовать принципы значения взаимного соседства (mnv) или k ближайших соседей. Первый подход – более динамический, независимый, второй – более производительный, но опирается на заданное статически число k. Использование динамических параметров при определении глобального сходства объектов позволит находить кластеры различной плотности в одном наборе данных.
|
|
|
Во-вторых, непосредственное сходство объектов, что позволит избежать проблем с заданной априорно моделью связности и соседства.
В-третьих, при вычислении близости кластеров, необходимо учитывать их внутреннюю связность и сходство. В этом смысле наиболее перспективным является подход, предложенный в алгоритме CHAMELEON. Соответствующие значения взаимной связности и сходства следует разделять на средние между двумя рассматриваемыми кластерами значения внутренней связности и сходства. Этот подход несколько отличается от используемого в ROCK, поскольку основан не на ожидаемом количестве связей (функция от размера), то есть определяется не статически.
Все эти принципы реализованы в алгоритме CHAMELEON, который использует меру объединения, сходства кластеров основанную на произведении связности и сходства двух кластеров. Однако, этот алгоритм мало изучен и проверен на практике. Главное его преимущество, помимо использования вышеозначенных принципов в применении чрезвычайно производительных методов разделения графа (мультиуровневое разделение).
Для нашей задачи, тем не менее, представляется наиболее перспективным использование именно этого алгоритма. Причем, возможно использовать как предложенный изначально вариант с разделением графа, построенного по принципу k ближайщих соседей, так и использовать значение взаимного соседства. Для этого значения, в частности, можно установить определенный порог на основе которого также выделить связи и уже использовать их веса для подсчета сходства. Можно статически заданный порог не устанавливать и использовать для вычисления взаимного и внутреннего сходства все попарные значения близости (то есть, фактически, применять метод попарного среднего).
Последний подход, очевидно, понизит производительность метода, хоть и позволит полностью отказаться от заданных параметров. Если, все-таки, как утверждается многими специалистами, подобный «динамический» порог не будет оказывать отрицательного влияния на результаты анализа и его можно будет подбирать оптимально для конкретного набора данных, то данное ограничение в виду его незначительности можно ввести в окончательный вариант алгоритма кластерного анализа.
|
|
|
В зависимости от используемой модели можно определить оптимальное соотношение глобального и локального сходства в определении близости кластеров (параметр a а произведении относительных сходств).
 2015-04-01
2015-04-01 996
996








