2015-04-01
1906
Функционально полной будет любая система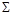 
, через функции которой можно выразить дизъюнкцию, конъюнкцию и отрицание. Действительно, для любой логической функции 
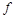представляющую ее формулу над 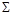, можно построить следующим образом: взять булеву формулу для 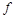(по теореме 4.2 такая формула обязательно найдется), и все булевы операции в ней заменить формулами над 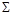, представляющими эти операции. Аналогично доказывается и более общее утверждение: если все функции функционально полной системы 
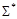представимы формулами над системой 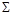, то 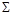также функционально полна. В этом случае говорят, что 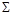сводится к .
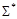В гл.2 система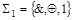 
была сведена к системе 
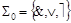, тем самым была доказана функциональная полнота 
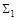. Рассмотрим еще ряд примеров доказательства полноты системы логических функций путем ее сведения к заведомо функционально полной системе.
Пример. Доказать функциональную полноту систем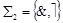 
и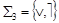 
.
Из законов де Моргана и двойного отрицания следует, что в каждой из этих двух систем недостающая до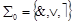 
функция выражается через две остальные:
,
.
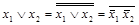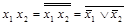Булева формула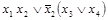 
в системе 
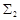перейдет в формулу 
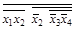, а в системе 
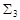– в формулу 
.
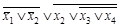Пример. Системы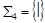 
(штрих Шеффера) и 
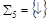(стрелка Пирса) функционально полны:
; 
;
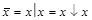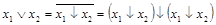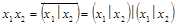
Следовательно,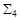 
сводится к 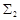, а 
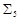– к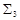 
(полнота 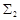и 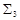доказана в предыдущем примере).
