Положительно и отрицательно определенные квадратичные формы

Квадратичная форма F(x) называется положительно определенной, если F(x) на каждом ненулевом векторе a больше 0, т.е. F(a) >0, если a¹ 0, aÎRⁿ. Если же F(a) <0 " a¹ 0, то квадратичная форма называется отрицательно определенной.

Теорема. Дана квадратичная форма F(x)=x(Ax), 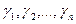– ее канонический базис, а выражение 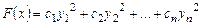, 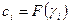– канонический вид формы в базисе .

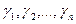Тогда справедливы следующие утверждения:

1. Квадратичная форма 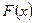является положительно определенной тогда и только тогда, когда 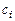>0 .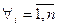

2. Квадратичная форма 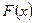является отрицательно определенной тогда и только тогда, когда 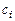<0 .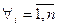

3. Квадратичная форма положительно определена, если все собственные значения ее матрицы положительны.

Справедливы следующие утверждения:

1. Квадратичная форма 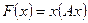положительно определена тогда и только тогда, когда главные миноры 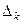матрицы положительны.

2. Квадратичная форма 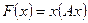отрицательно определена тогда и только тогда, когда все главные миноры матрицы нечетного порядка отрицательны, а все главные миноры четного порядка – положительны.