Тренировочные задания. 1. Уравнение ТП (1.1.2) для m = 1 имеет вид

1. Уравнение ТП (1.1.2) для m = 1 имеет вид

S_t = a S_{t -1} + b C_t + H_t,

Предположим, что данное уравнение описывает рост биомассы (концентрации) S некоторого основного ингредиента вещества под воздействием дополнительного ингредиента вещества, имеющего концентрацию C. Пусть в начале процесса концентрация основного вещества равна S ₀, а концентрация дополнительного ингредиента равна C ₀. При этом концентрация дополнительного ингредиента убывает со временем t (t = 1, 2, 3, … T) по линейному закону

C _t = C ₀ – g t.

Покажите, что зависимость S_t от b, C ₀, g и T при a = 1 выражается как

S_T = S ₀ + b C ₀ T – bg T (T +1)/2 + .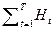

Указание. Воспользуйтесь последовательной подстановкой значений t = 1, 2, 3, … T в уравнение ТП и формулой суммы членов арифметической прогрессии 1+2+3+… + T = T (T +1)/2.

2. Покажите, что зависимость S_t от b, C ₀, g и T при произвольном a выражается как

S_T = a ^T S ₀ + b C ₀[1+ a + a ² +…+ a ^{T- 1}]–

– bg [ a ^{T- 1}+2 a ^{T- 2}+3 a ^{T- 3} +…+(T –1) a + T ] + .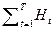

3. Преобразуйте полученное в 2 выражение, воспользовавшись формулой геометрической прогрессии

a ⁰ + a¹ + a² + … + a ^{T- 1} = .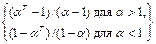

4. Найдите значение концентрации S основного ингредиента к моменту исчезновения дополнительного ингредиента при a = 1. Покажите при каких значениях g будет наблюдаться прирост концентрации основного ингредиента.

5. Дайте объяснение полученной модели ТП и смысла коэйффициентов a, b и g. Постройте примерную диаграмму ТП (см. рис.1.2.1).

6. Воспользовавшись правилом расчета дисперсий (см. стр. 27) покажите, что для ú a ú < 1 ошибка (дисперсия s_S ² = = var (S)) определения ТП S_t имеет вид

var (S) = [ b ² g ² T ² /12+ s_H ²]/(1– a ²),

если помеха некоррелирована c ТП, т.е., cov (S_t, H_t) = 0и cov (С_t, H_t) = 0, а такжеимеет дисперсию var (H_t, H_t) = s_H ².

Указание. var (t) = T ² /12.

Тесты по темам модуля

(выбрать правильный ответ/ответы из 3-х предлагаемых)

1. Состоянием (вектором состояния) технологического

процесса (ТП) называется:

1.1 зависимость от времени целенаправленно изменяемых параметров материальных, финансовых и информационных потоков, определяющих направленность технологического процесса;

1.2 совокупность изменяемых во времени основных параметров технологического процесса;

1.3 совокупность таких переменных, знание которых, наряду с векторами управления и структурных параметров, а также уравнениями, описывающими динамику ТП, позволяют определять его будущее.

2. Структурой (вектором структурных параметров) ТП

называется:

2.1 совокупность параметров, описывающих как внутренние, так и внешние организационные связи ТП;

2.2 совокупность параметров, описывающих внутренние и внешние связи ТП без учета их иерархии;

2.3 совокупность параметров описывающих все связи ТП.

3. Управлением состоянием ТП называется процесс:

3.1 изменения параметров ТП во времени;

3.2 целенаправленное изменение состояний ТП;

3.3 целенаправленное изменение основных параметров ТП.

4. Оптимальным называется управление, при котором:

4.1 задано уравнение состояний ТП;

4.2 заданы целевые критерии управления в виде функционалов, зависящих от состояний ТП;

4.3 задано уравнение состояний ТП и функциональные ограничения на состояния.

5. Фазовой траекторией состояний управляемого ТП

называется:

5.1 зависимость параметров состояний от времени;

5.2 кривая, описывающая критерий управления в зависимость от параметров его состояний;

5.3 кривая, неявно зависящая от времени, каждая точка которой задается совокупностью параметров состояний ТП.

6. Условно-оптимальное управление ТП отличается от

оптимального тем, что:

6.1 используются специальные целевые критерии и ограничения состояний ТП;

6.2 используются целевые критерии и ограничения, зарекомендовавшие себя на практике и связанные с отдельными финансовыми и материальными компонентами состояний ТП при заданных ограничениях;

6.3 используются ограниченное число критериев оптимальности.

7. Критерием среднеквадратичного отклонения траекторий для однопараметрического фазового пространства

называется:

7.1 å _t (S_t) ²;

7.2 å _t (S_t – S^*_t) ²;

7.3 å _т å _t g_т (S_t – S^*_t) ².

8. Выборочной вероятностью наступления события

называется:

8.1. величина, задаваемая диапазонами значений,

соответствующих данному событию, и некоторыми

гипотетическими степенями принадлежности значений

этим диапазонам;

8.2. отношение числа случаев, когда это событие наступило

при испытании, к общему числу всевозможных случаев в

испытании;

8.3. частота, описываемая статически обоснованными законами распределения.

9. Плотностью распределения вероятностей называется:

9.1. производная функция распределения;

9.2. вероятность того, что она примет значение, не

превосходящее некоторое заданное;

9.3. интеграл функции распределения.

10. Оценка выборочного среднего является эффективной,

если:

10.1. она равна теоретическому математическому ожиданию;

10.2. дает точные значения для больших выборок, независимо от входящих в них конкретных наблюдений;

10.3. ее дисперсия минимально возможна.

11. Коэффициент корреляции случайных величин X и Y

определяется выражением:

11.1. r _XY = s _XY / (s ² _X s ² _Y)^1/2;

11.2. r _XY = s _XY / (s ² _X s ² _Y);

11.3. r _XY = (s ²_X s ²_Y)^1/2/ s _XY.

12. Для проверки репрезентативности однородной выборки нормально распределенной генеральной совокупности применяется:

12.1. коэффициент симметрии;

12.2. коэффициент асимметрии;

12.3. коэффициент эксцесса.

13. Коэффициент эксцесса определяется выражением:

13.1. e_X = [ 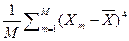/ 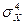] – 3;

13.2. e_X = [ 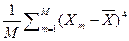/ 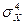] – 1;

13.3. e_X = [ 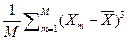/ 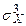] – 3.

14. Коэффициент асимметрии определяется выражением:

14.1 Sk_X = / .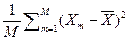

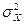14.2 Sk_X = / .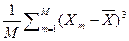

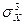14.3 Sk_X = / ,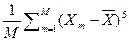

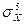15. Мерой неопределенности является:

15.1. информация;

15.2. вероятность;

15.3. энтропия.

16. Вероятностное распределение отличается от нечеткого:

16.1. знанием закона распределения;

16.2. диапазонами задания распределения;

16.3. знанием числовых характеристик распределения.