Движение подземных вод в безнапорном пласте

Рассмотрим установившееся движение воды в условном потоке с горизонтальным водоупором при постоянном расходе потока. В сечениях 1 и 2 напоры соответственно равны Н₁ и Н₂ (рис.6). Напишем дифференциальное уравнение Дюпюи для промежуточного сечения, взятого на расстоянии х от начала координат, .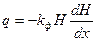

В отличие от выражения 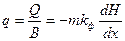, где мощность постоянная, в данном случае она является переменной и при принятой плоскости сравнения напоров (горизонтальный водоупор) численно равна напору.

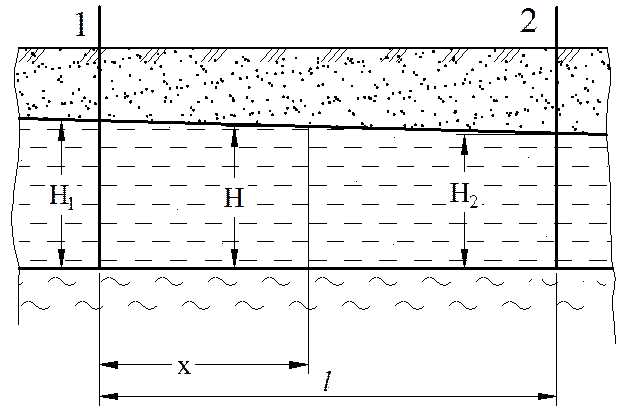
Рис. 6. Схема движения подземных вод в безнапорном пласте при горизонтальном залегании водоупора

Разделяя переменные и интегрируя в пределах от сечения l до сечения 2 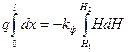, получим формулу для определения единичного расхода потока 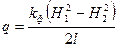. Разложив разность квадратов и имея в виду, что 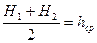; 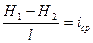, получим 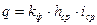, где 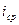- средний уклон депрессионной кривой между сечениями 1 и 2; 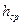- средняя мощность водоносного пласта на участке между этими сечениями.

Расход потока при его ширине В равен .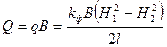

Если известны уровни воды в скважинах, расположенных вдоль потока, то можно построить депрессионную кривую между ними.

Напишем уравнение для единичного расхода потока через известный напор Н₁ и неизвестный напор Н в сечении на расстоянии х от начала координат: .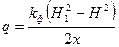

При постоянном расходе q левые части выражений единичных расходов 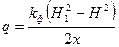и 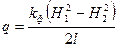равны, а следовательно, равны и правые: 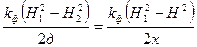, отсюда 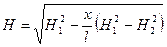. Задаваясь любыми значениями х в пределах х<l и получая соответствующие им значения Н, можно по точкам построить депрессионную кривую между скважинами. Эта кривая является параболой.