Пусть у нас функции выигрышей игроков и управления имеют следующую зависимость:
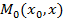 ,
, 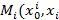 ),где
),где 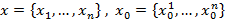 . Будем считать, что
. Будем считать, что 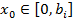 -выплаты центра
-выплаты центра 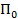 элементу
элементу 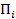 за произведенную продукцию
за произведенную продукцию 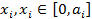 .
.
Пусть выполнены условия монотонности.
Функция 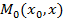 строго монотонно растет по
строго монотонно растет по 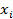 , а по
, а по 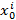 - строго монотонно убывает. Аналогично
- строго монотонно убывает. Аналогично 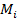 от любого поощрения
от любого поощрения 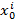 строго монотонно растет, а от затрат убывает.
строго монотонно растет, а от затрат убывает.
Очевидно 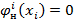 – стратегия наказания центра.
– стратегия наказания центра.
Максимальные гарантированные результаты подчиненных равны 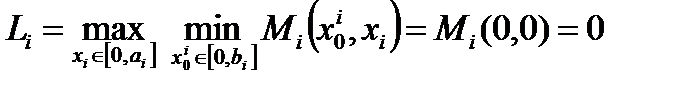
Заметим, что ситуация (0,0) является ситуацией равновесия по Нэшу на классе управлений. Пусть точка 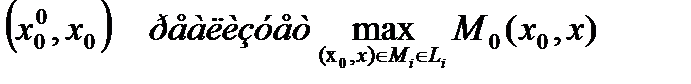 ,где взаимовыгодное множество D определяется ограничением
,где взаимовыгодное множество D определяется ограничением 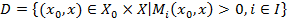 . Тогда оптимальная стратегия будет выглядеть следующим образом:
. Тогда оптимальная стратегия будет выглядеть следующим образом:
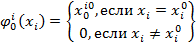
 2015-04-01
2015-04-01 384
384








