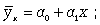Прямолинейная

(8.1)

криволинейная в виде:

параболы второго порядка (или высших порядков)

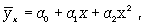(8.2)

гиперболы

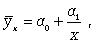(8.3)

показательной функции

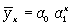(8.4)

и т.д.

Параметры для всех этих уравнений связи, как правило, определяют из системы нормальных уравнений, которые должны отвечать требованию метода наименьших квадратов (МНК):

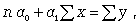
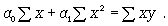(8.5)

Если связь выражена параболой второго порядка (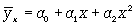), то систему нормальных уравнений для отыскания параметров a₀, a₁, a₂ (такую связь называют множественной, поскольку она предполагает зависимость более чем двух факторов) можно представть в виде

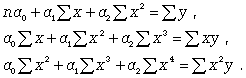(8.6)

Другая важнейшая задача - измерение тесноты зависимости - для всех форм связи может быть решена при помощи вычисления эмпирического корреляционного отношения :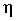

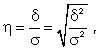(8.7)

где - 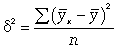дисперсия в ряду выравненных значений результативного показателя 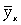; 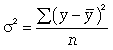- дисперсия в ряду фактических значений у.

Для определения степени тесноты парной линейной зависимости служит линейный коэффициент корреляции r, для расчета которого можно использовать, например, две следующие формулы:

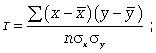(8.8)

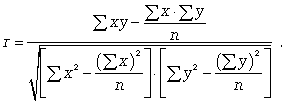
Линейный коэффициент корреляции может принимать значения в пределах от -1 до + 1 или по модулю от 0 до 1. Чем ближе он по абсолютной величине к 1, тем теснее связь. Знак указывает направление связи: «+» - прямая зависимость, «-» имеет место при обратной зависимости.

8.3.