Основные понятия и определения теории графов

Тема 3. ГРАФЫ

Графы и их представление в памяти ЭВМ.

Основные понятия и определения теории графов

Теория графов представляет собой раздел математики, имеющий широкое практическое применение. В её терминах формулируется большое число задач, связанных с дискретными объектами. Такие задачи возникают при проектировании интегральных схем и схем управления, электрических цепей, блок-схем программ, в экономике, статистике, химии, биологии и в других областях. Теория графов становится одной из существенных частей математического аппарата кибернетики, языком дискретной математики.

В отличие от других научных дисциплин, теория графов имеет вполне определенную дату рождения. Первая работа по теории графов, написанная швейцарским математиком Леонардом Эйлером (1707-1783), была опубликована в 1736 году в Трудах Академии наук в Санкт-Петербурге. Исследование Эйлера было проведено в связи с популярной в то время задачей о кенигсбергских мостах. Эта задача имеет следующую формулировку:

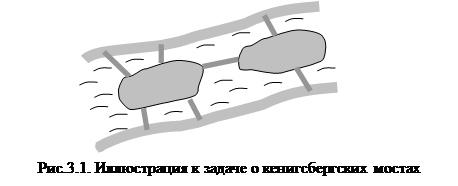
Задача 1. Город Кенигсберг, располагавшийся в восточной Пруссии, был построен в месте слияния двух рек на их берегах и на двух островах. В городе было семь мостов, которые соединяли острова между собой и с береговыми частями города (рис.3.1). Необходимо ответить на вопрос: мог ли любой житель Кенигсберга, выйдя из дома, пройти по всем семи мостам города в точности по одному разу и вернуться домой?

Ответ на вопрос, поставленный в данной задаче, должен быть отрицательным. Эйлер дал этот ответ и нашел критерий существования маршрута, удовлетворяющего требованиям задачи.

Однако результат, полученный Эйлером, более ста лет оставался единственным результатом теории графов.

Развитие теории графов в конце XIX и начале XX вв. было связано с распространением представлений о молекулярном строении вещества и становлением теории электрических цепей. К 50-м годам нашего века в теории графов сложились два различных направления: алгебраическое и оптимизационное.

Например, поиск ответа на поставленный в задаче 1 вопрос относится к алгебраическому направлению теории графов. Изменим задачу 1.

Задача 2. Отличие задачи 2 от задачи 1 состоит в том, что требуется найти маршрут, по которому житель, выйдя из дома, пройдет по каждому мосту хотя бы один раз и вернется домой, причем длина маршрута должна быть минимальной.

Задача поиска такого маршрута относится к оптимизационному направлению теории графов.

Итак, первая работа по теории графов принадлежит Л.Эйлеру, и опубликована она была в 1736 г., однако термин “граф” впервые появился в книге венгерского математика Д. Кенига в 1936 г.

Дадим определение графа. Пусть V - непустое множество, V ^{2} - множество всех его двухэлементных подмножеств. Пара (V, E), где Е Í V ^{2} называется графом (неориентированным графом).

Граф называется конечным, если множество V конечно. В дальнейшем под термином “граф” будем понимать конечные графы.

Элементы множества V называются вершинами графа, а элементы множества Е называют рёбрами графа.

Число вершин графа G =(V, E) называется его порядком.

Исходя из определения графа, каждому ребру соответствует двухэлементное подмножество вершин. Если подмножество { v ₁, v ₂} соответствует ребру е, то говорят, что ребро е инцидентно вершинам v ₁ и v ₂, а вершины v ₁ и v ₂ смежны. Также говорят, что ребро е соединяет вершины v ₁ и v ₂. Вершины v ₁ и v ₂ называются концевыми вершинами ребра е.

Граф можно представить графически: каждая вершина представляется точкой или окружностью, а каждое ребро представляется отрезком, соединяющим его концевые вершины.

Граф G =(V, E), V ={ v ₁, v ₂, v ₃, v ₄}, E ={{ v ₁, v ₂}, { v ₁, v ₄}, { v ₂, v ₃}, { v ₂, v ₄}, { v ₃, v ₄}} представлен графически на рис.3.2.

Обобщим понятие графа.

Мультиграф – это пара (V, E), где V - непустое множество, а E - семейство подмножеств множества V ^{2}.

Употребление термина “семейство” вместо “подмножество” означает, что элементы множества V ^{2} могут в E повторяться, то есть допускаются кратные рёбра.

Пример мультиграфа показан на рис. 3.3.

Дальнейшее обобщение состоит в том, что кроме кратных рёбер допускаются еще петли, то есть рёбра, соединяющие вершину саму с собой.

Такой граф называется псевдографом. Его пример приведен на рис. 3.4.

Псевдограф – это пара (V, E), где V - непустое множество (вершин), а E - некоторое семейство неупорядоченных пар вершин (рёбер), не обязательно различных.

Различают также ориентированные и смешанные графы.

Пусть V ⁽²⁾ - множество упорядоченных пар элементов множества V. Тогда ориентированный граф (или орграф) - это пара (V, А), где V - множество вершин, А Í V ⁽²⁾ - множество ориентированных рёбер, которые называются дугами.

Если пара (v ₁, v ₂) - дуга, то вершины v ₁ и v ₂ называются её началом и концом соответственно.

На рисунке дуги отмечаются стрелками, указывающими направление от начала к концу.

Орграф G =(V, E), V ={ v ₁, v ₂, v ₃, v ₄}, E ={(v ₁, v ₂), (v ₁, v ₄), (v ₂, v ₃), (v ₂, v ₄), (v ₃, v ₄)} представлен графически на рис.3.5.

Ориентированный мультиграф и ориентированный псевдограф определяются аналогично.

Смешанные графы имеют как дуги, так и неориентированные рёбра.

Пример смешанного графа представлен на рис. 3.6.

Ради сокращения речи термин “граф” употребляется вместо терминов “мультиграф”, ”орграф” и др., но подобные случаи либо специально оговариваются, либо ясны из контекста.

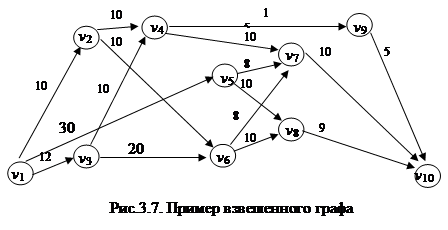
Часто каждой дуге графа ставят в соответствие одно или несколько чисел. Такой граф называется взвешенным (или сетью). Пример взвешенного графа представлен на рис. 3.7.

Рассмотрим некоторые понятия теории графов. Отметим, что многие понятия не являются устоявшимися, и могут в различной литературе определяться неодинаково.

Пусть v ₁, v ₂,…, v_n, v_{n +1} - произвольная последовательность вершин орграфа.

Цепью называется любая последовательность дуг e ₁, e ₂,..., e_n, такая, что концевыми вершинами дуги e_i являются вершины v_i и v_{i +1}, то есть e_i =(v_i, v_{i +1}) или e_i =(v_{i +1}, v_i) для i =1,2,…, n.

Цепь, для которой e_i =(v_i, v_{i +1}) при всех i =1,2,…, n, называется путём.

Циклом называется цепь, у которой начальная и конечная вершины совпадают.

Контуром называется путь, у которого начальная и конечная вершины совпадают.

Цепь, путь, цикл или контур называются простыми, если они не содержат внутри себя циклов.

У графа, изображенного на рис. 3.8.

- дуги (v ₂, v ₁), (v ₂, v ₂), (v ₃, v ₂), (v ₃, v ₄) образуют цепь, соединяющую вершину v ₁ с вершиной v ₄;

- дуги (v ₂, v ₂), (v ₂, v ₄), (v ₄, v ₃) образуют путь, соединяющий вершины v ₂ и v ₃;

- дуги (v ₃, v ₂), (v ₂, v ₄), (v ₃, v ₄) образуют цикл с начальной и конечной вершиной v ₃;

- дуги (v ₃, v ₂), (v ₂, v ₄), (v ₄, v ₃) образуют контур с начальной и конечной вершиной v ₃;

- цепь (v ₂, v ₁), (v ₃, v ₂), (v ₃, v ₄), (v ₄, v ₃) с начальной вершиной v ₁ и конечной v ₃ не является простой, так как содержит внутри себя цикл (v ₃, v ₄), (v ₄, v ₃).

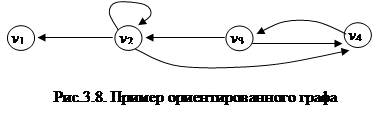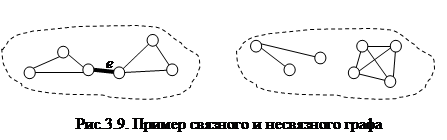
Граф называется связным, если в нем для каждой пары вершин найдётся соединяющая их цепь.

Связный и несвязный граф представлен на рис.3.9.

Любой граф можно рассматривать как некоторую совокупность связных графов. Каждый из этих графов называется компонентом исходного графа.

Несвязный граф, изображённый на рис. 3.9, имеет два компонента.

Множество дуг, исключение которых из графа увеличивает число его компонентов, называется разрезом.

Для связного графа, изображенного на рис. 3.9, разрезом является выделенная дуга e, так как её удаление увеличивает число компонентов до двух.

Пусть G =(V, E), V ¢Í V, тогда граф, множество вершин которого совпадает с V ¢, а множество дуг включает все дуги множества E с концевыми вершинами в V ¢, называется подграфом графа G, порождённым V ¢.

Пусть E ¢Í E, тогда граф, для которого множество дуг совпадает с E ¢, а множество вершин включает вершины, инцидентные дугам из E ¢, называется подграфом графа G, порождённым E ¢.

Граф называется полным,если любые две его вершины смежные.

Граф G называется пустым, если в нём нет рёбер.

Граф, который не содержит циклов, называется ациклическим.

Связный неориентированный ациклический граф называется деревом, множество деревьев называется лесом.

Если рёбра, составляющие дерево, заменить ориентированными дугами, то получим ориентированное дерево. Если из контекста ясно, о каком дереве идет речь, то в дальнейшем слово «ориентированное» будем опускать.

Для ориентированного дерева имеет смысл ввести понятие корня. Минимальное по мощности множество вершин ориентированного дерева, из которых существуют пути во все оставшиеся вершины, будем называть множеством корней.

Покрывающим (остовным) деревом графа G называется дерево, являющееся подграфом графа G и содержащее все его вершины.

Если граф G несвязен, то множество, состоящее из основных деревьев каждой компоненты, называется покрывающим (остовным) лесом.

Обобщением графа является гиперграф.

В гиперграфе, в отличие от графа, рёбрами могут быть не только двухэлементные, но и любые подмножества вершин.

Подобные объекты в математике известны давно, однако введение термина “гиперграф” связано с успешным рассмотрением на них ряда важных понятий и методов теории графов.

3.1.2. П редставление графов в памяти ЭВМ

Любой граф может быть представлен в матричной форме.

Матрицей смежности графа G= (V,E)называется матрица A порядка n´n, где n=|V|. Элемент матрицы смежности а_ij= 1, если (v_i,v_j)Î Е, v_i,v_j Î V и a_ij= 0, если (v_i,v_j)Ï Е.

Для графа, изображенного на рис. 3.5, матрица смежности представлена в таблице 3.1.

Отметим, что для неориентированных графов матрица смежности симметрична относительно главной диагонали, то есть в памяти ЭВМ достаточно хранить только половину матрицы.

Таблица 3.1.

Матрица смежности графа, изображенного на рис.3.5

Матрицей инцидентности графа G =(V, E) называется матрица B порядка n ´ m, где n =| V |, m =| E |. Элементы матрицы инцидентности b_ij определяются следующим образом: b_ij =1, если i -я вершина является началом j -ой дуги, b_ij =-1, если i -я вершина является концом j -ой дуги, b_ij =0, если i -я вершина и j -я дуга не инцидентны.

Для неориентированных графов в матрице инцидентности элементам достаточно присваивать только два символа (1 и 0).

Для графа, представленного на рис. 3.5, матрица инцидентности показана в таблице 3.2.

Таблица 3.2.

Матрица инцидентности графа, изображенного на рис.3.5

-1
		-1
	-1		-1	-1

Заметим, что с помощью матрицы инцидентности не могут быть закодированы петли графа. В свою очередь в матрице смежности теряется информация о кратных рёбрах (дугах). Поэтому в некоторых случаях требуется отходить от определений и вводить дополнительные структуры данных для хранения кратных рёбер и петель.

При кодировании взвешенного графа вместо единичных элементов матрицы смежности удобно записать веса соответствующих дуг, а веса несуществующих дуг полагать равными ¥. Такая матрица называется матрицей весов.

Матрица весов для графа, представленного на рис.3.7, приведена в таблице 3.3.

Таблица 3.3.

Матрица весов графа, изображенного на рис.3.7

¥			¥		¥	¥	¥	¥	¥
¥	¥	¥		¥		¥	¥	¥	¥
¥	¥	¥		¥		¥	¥	¥	¥
¥	¥	¥	¥	¥	¥		¥		¥
¥	¥	¥	¥	¥	¥			¥	¥
¥	¥	¥	¥	¥	¥			¥	¥
¥	¥	¥	¥	¥	¥	¥	¥	¥
¥	¥	¥	¥	¥	¥	¥	¥	¥
¥	¥	¥	¥	¥	¥	¥	¥	¥
¥	¥	¥	¥	¥	¥	¥	¥	¥	¥

На практике очень часто матрицы, представляющие графы, бывают сильно разряженными, то есть содержат много символов “0” или “¥”. Это приводит к неоправданным затратам памяти при хранении этих матриц в ЭВМ.

Объем памяти можно существенно уменьшить, если упаковывать матрицы в списки гнездового типа.

Пример упаковки рассмотренной матрицы весов (табл. 3.3) в список гнездового типа, реализованный на трех векторах (массивах), приведен на рис.3.10.

Для нахождения вершин, смежных i –ой вершине, и весов соответствующих дуг по такой структуре необходимо вычислить начальный In и конечный Ik индексы в векторах V и S по формулам

In=U_i

Ik=U_{i +1}-1.

Тогда S_In, S_In+1,…, S_Ik - вершины, смежные i -ой вершине, V_In, V_{In +1},…, V_Ik – длины дуг (i, S_In),(i, S_{In +1},),…,(i, S_Ik).

Для хранения упакованной таким образом матрицы весов понадобится 42 ячейки памяти, занимаемых массивами V, S и U. Неупакованная матрица занимала 10´10=100 ячеек памяти.

V

S

U

Рис.3.10. Упаковка матрицы весов (табл. 4.3) в список гнездового типа

При реализации алгоритмов, в которых изменяется исходный граф (добавляются или удаляются вершины и так далее), для хранения графов иногда удобно применять списки смежности. Список смежности можно реализовать путем создания линейного списка из n линейных списков, где n – число вершин графа.

Для графа, изображенного на рис. 3.7, список смежности представлен на рис. 3.11.

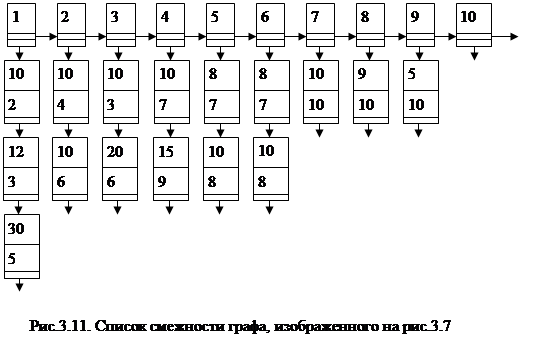Еще один способ хранения графов - это список рёбер, то есть список, в котором перечислены все рёбра графа.

Список рёбер графа, представленного на рис. 3.7, приведен на рис. 3.12.

Список рёбер реализован на трех массивах и занимает 48 ячеек. Можно также вместо массивов использовать списковые структуры.

Выбор того или иного способа кодирования графа и структуры данных для его реализации зависит как от конкретной задачи, алгоритма её решения, возможных входных данных, так и от индивидуальных наклонностей программиста.

I

J

V

I - начальная вершина, J – конечная вершина, V – вес дуги (I, J)

Рис.3.12. Список рёбер графа, изображенного на рис.4.7