Понятия модели и моделирования

Математические модели в науке как средство работы с информацией

Невозможно представить себе современную науку без широкого применения математического моделирования, суть которого состоит в замене исходного объекта его образом – математической моделью и дальнейшем изучении модели с помощью реализуемых на компьютерах вычислительно-логических алгоритмов. Этот метод сочетает в себе достоинства, как теории, так и эксперимента, поскольку работа не с самим объектом (явлением, процессом), а с его моделью дает возможность относительно быстро и без существенных затрат исследовать его свойства и поведение в различных ситуациях. В то же время вычислительные эксперименты с моделями объектов позволяют, опираясь на мощь современных вычислительных методов и технических средств информатики, подробно и глубоко изучать объекты в достаточной полноте, недоступной чисто теоретическим подходам.

Вышесказанное является актуальным в условиях постоянного роста требований к эффективности устройств, применяемых в системах передачи и обработки информации, к сокращению сроков исследования и разработки новых телекоммуникационных систем и сетей.

Моделирование можно рассматривать как замещение исследуемого объекта (оригинала) его условным образом, описанием или другим объектом, именуемым моделью и обеспечивающим близкое к оригиналу поведение в рамках некоторых допущений и приемлемых погрешностей. Моделирование обычно выполняется с целью познания свойств оригинала путем исследования его модели, а не самого объекта. Разумеется, моделирование оправдано в том случае когда оно проще создания самого оригинала или когда последний по каким-то причинам лучше вообще не создавать.

МОДЕЛЬ ("модель" от лат. "modelus", что означает "мера") - мысленно предста­вимая или материально реализованная система, которая, отражая и воспроиз­водя объ­ект исследования, способна замещать его при определенных условиях так, что изуче­ние ее дает новую информацию об этом объекте. М. в самом широком смысле - это любой мысленный или знаковый образ моделируемого объекта (оригинала).

Таким образом, под моделью мы будем понимать совокупность объектов (понятий, свойств, признаков, знаков, геометрических элементов, материальных предметов) и отношений между ними (называемых моделирующими), которые выражают существенные с точки зрения цели моделирования стороны изучаемого объекта, явления или процесса. Короче, модель - это некоторое упрощённое подобие реального объекта, процесса или явления.

М. строится для достижения определенной цели, однако для одного и того же объ­екта можно построить, преследуя одну и ту же цель, разные модели. Поэтому можно считать, что М. некоторого объекта А (оригинала, прототипа) – это объект В, в каком-то отноше­нии подобный (аналогичный) оригиналу А, но отличающийся от него, вы­бранный или по­строенный, по крайней мере, для одной из следующих целей:

1) замена оригинала А моделью B в некотором реальном или воображаемом дейст­вии, ис­ходя из того, что В более удобна для осуществления этого действия в данных условиях (т.н. называемая модель-заместитель);

2) создание наглядного представления об объекте А (реально существующем или вообра­жаемом) с помощью объекта В (т.н. называемая модель-представление);

3) истолкование (интерпретация) объекта А в виде модели В (т.н. называемая мо­дель-ин­терпретация);

4) исследование (изучение) объекта А посредством изучения объекта В (т.н. назы­ваемая исследовательская модель).

Пример.1. В курсе математики представлены все перечис­ленные виды мо­делей. Так, уравне­ние, со­ставленное по условию текстовой задачи, вы­сту­пает как модель-заместитель исходной задачи; чер­теж некоторого геометрического объекта, построенный для доказательства утверждения, в кото­ром идет речь в этом утверждении, яв­ляется моде­лью-представлением рассматриваемого объекта; урав­нение (x – a)² + (y – b)² = R ² является моделью-интерпретацией окружности.

М. обычно обладает не одним каким-либо признаком, соответствующим одной из указанных целей, а несколькими, и поэтому она пригодна, как правило, и для других целей. Например, модель-заместитель может использоваться и как модель-представ­ление, и как мо­дель-интерпретация, и как исследовательская модель. Так, модель-ин­терпретация окружно­сти вполне пригодна для исследования свойств окружности, а, значит, она является и моде­лью исследовательской.

По способу построения модели бывают материальные и идеальные. В качестве ма­тери­альных моделей могут выступать копии оригинала (уменьшенные или увеличен­ные), причем они могут быть динамические и статические; в качестве идеальных - изображения, описа­ния, схемы, чертежи, графики, уравнения, планы, карты, компью­тер­ные программы и т.д.

Пример 2. В медицине многие лекарственные препараты, разрабатывае­мые для лечения людей, первоначально испытывают на животных, которые в этом случае и выступают в качестве модели че­ловека; моделью некоторой местности может служить географическая карта, пользуясь которой, мы получаем нужную нам информацию об этой местности; моделью прямолиней­ного равномерного движения служит уравнение s = v ₀ +vt, исследование ко­торого дает воз­можность устанавливать ос­новные закономерности данного вида движения; моделью неко­торого предмета, явления, процесса или ситуации (как реальных, так и «вирту­альных») могут служить компьютерные программы, пре­доставляющие в распоряжение ис­следователя прак­тически неограниченные возможности для их изу­чения и прогнозирования развития; и т.п.

М. всегда является лишь ото­бражением оригинала, и она в каком-либо отношении должна быть не только удобна для изучения свойств исследуемого объекта, но и по­зволяет перенести по­лученные при этом знания на исходный объект. Например, когда в начальных школе учитель намеревается более наглядно продемонстрировать способ сложения нату­ральных чисел, то он использует для этого различные модели этих чи­сел: реальные пред­меты или их изображения, абак, русские счеты, и др. Многие дет­ские игрушки, пред­ставляющие собой модели реальных объектов (автомобилей, по­ездов, животных и т.п.), позволяют ребенку познавать определенные свойства окру­жающих его предметов.

М. строится с тем расчетом, чтобы охватить только те свойства ориги­нала, которые существенны в данной ситуации и являются объектом изучения. Например, сущест­вует разнообразные модели обучения математике; одни из них позволяют исследо­вать сте­пень усвоения материала, другие – познавательную активность, третьи - твор­ческую матема­тическую деятельность, и т.д. Для изучения поведения проектируемого самолета в воздухе строят уменьшенную во много раз его модель и помещают ее в аэродинамическую трубу. Затем по поведению этой модели в различных воздушных потоках, создаваемых в трубе, судят о том, как будет вести себя в полете настоящий самолет.

М., полностью воспроизводящая оригинал, перестает быть моделью.

Существует ряд общих требований к моделям:

1. Адекватность – достаточно точное отображение свойств объекта;

2. Полнота – предоставление получателю всей необходимой информации об объекте;

3. Гибкость – возможность воспроизведения различных ситуаций во всем диапазоне изменения условий и параметров;

4. Трудоемкость разработки должна быть приемлемой для имеющегося времени и программных средств.

Моделирование – это процесс построения модели объекта и исследования его свойств путем исследования модели.

Таким образом, моделирование предполагает 2 основных этапа:

1. Разработка модели;

2. Исследование модели и получение выводов.

При этом на каждом из этапов решаются разные задачи и используются отличающиеся по сути методы и средства.

Метод моделирования во многих науках является средством, позволяющим ус­та­навли­вать более глубокие и сложные взаимосвязи между теорией и опытом и способ­ным заменить эксперимент.

Целый ряд исследований вообще невозможен без моде­лирования, по­тому, что:

а) эксперименты могут проводиться лишь на ныне существующих объектах, т.к. невоз­можно распространить эксперимент в область прошлого;

б) вмешательство в некоторые системы иногда имеет такой характер, что невоз­можно ус­тановить причины появившихся изменений (вследствие вмешательства или по другим при­чинам);

в) некоторые теоретически возможные эксперименты неосуществимы вследствие низ­кого уровня развития экспериментальной техники или ее высокой стоимости;

г) большую группу экспериментов, связанных с человеком, сле­дует отклонить по мо­рально-этическим соображениям.

Однако М. находит широкое применение не только из-за того, что может за­менить эксперимент.

Оно имеет большое самостоятельное значение и свои преимущества:

1. С помощью метода моделирования на одном комплексе данных можно разрабо­тать целый ряд различных моделей, по-разному интерпретировать исследуемое явле­ние, и вы­брать наи­более плодотворную из них для теоретического истолкования.

2. В процессе построения модели можно сделать различные дополнения к иссле­дуемой ги­потезе и получить ее упрощение.

3. В случае сложных моделей можно применять компьютерную технику.

4. Существует возможность проведения модельных экспериментов. И др.

На практике применяют различные методы моделирования. В зависимости от способа реализации, все модели можно разделить на два больших класса: физические и математические.

Математическое моделирование принято рассматривать как средство исследования процессов или явлений с помощью их математических моделей.

Под физическим моделированием понимается исследование объектов и явлений на физических моделях, когда изучаемый процесс воспроизводят с сохранением его физической природы или используют другое физическое явление, аналогичное изучаемому. При этом физические модели предполагают, как правило, реальное воплощение тех физических свойств оригинала, которые являются существенными в конкретной ситуации. Например, при проектировании нового самолета создается его макет, обладающий теми же аэродинамическими свойствами; при планировании застройки архитекторы изготавливают макет, отражающий пространственное расположение ее элементов. В связи с этим физическое моделирование называют также макетированием.

Полунатурное моделирование представляет собой исследование управляемых систем на моделирующих комплексах с включением в состав модели реальной аппаратуры. Наряду с реальной аппаратурой в замкнутую модель входят имитаторы воздействий и помех, математические модели внешней среды и процессов, для которых неизвестно достаточно точное математическое описание. Включение реальной аппаратуры или реальных систем в контур моделирования сложных процессов позволяет уменьшить априорную неопределенность и исследовать процессы, для которых нет точного математического описания. С помощью полунатурного моделирования исследования выполняются с учетом малых постоянных времени и нелинейностей, присущих реальной аппаратуре. При исследовании моделей с включением реальной аппаратуры используется понятие динамического моделирования, при исследовании сложных систем и явлений - эволюционного, имитационного и кибернетического моделирования.

Очевидно, действительная польза от моделирования может быть получена только при соблюдении двух условий:

1. Модель обеспечивает корректное (адекватное) отображение свойств оригинала, существенных с точки зрения исследуемой операции;

2. Модель позволяет устранить перечисленные выше проблемы, присущие проведению исследований на реальных объектах

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ – приближенное описание ка­кого-либо явле­ния внешнего мира, выраженное с помощью математической сим­волики. Ма­тематиче­ские модели описываются с помощью средств самой математики: языка, понятий, отно­шений, теорий. В отличие от есте­ственнонауч­ных и гуманитарных дисциплин М.м. обычно не требует создания ма­териали­зованных объектов. Кроме то­го, если все дру­гие науки изу­чают модели, то ма­тематика изучает «модели моделей». Потому ее мате­риал в наилуч­шей степени соответствует задаче овладения методом моделиро­вания.

Примером М.м. достаточно сложно­го оригинала служит система уравне­ний (и не­равенств) в самом широком понимании. Система может содержать обыкновен­ные дифферен­циальные уравнения, уравнения в частных производных, интегральные уравнения, алгебраи­ческие и трансцендентные уравнения (и неравенства), набор ве­роятностно-статистических данных и т.д. К математическим моделям относят и про­граммы, составленные для ком­пьютеров, которые моделирую (отражают) оп­ределен­ные процессы, описанные средст­вами математики, положенными в основу ал­горит­мов.

Пример 3. Развитие ЭВМ и методологии системного анализа дало возможность для изуче­ния широкомас­штабных социальных процессов. Возникло так называемое глобальное моде­лирование и на его основе - прогно­зирование мировых социальных явлений.

Основоположником и «идейным отцом» такого рода исследований считается Дж. Форре­стер. В своей ра­боте “Мировая динамика” (1971 г.) он сделал успешную попытку использо­вать математиче­ские методы и ЭВМ для создания варианта модели экономического развития общества с учетом двух важнейших факторов - числен­ности населения и загрязнения окру­жающей среды. Расчеты показали, что при сохранении тенденций развития общества неиз­бежен серьезный кризис во взаимодействии человека и окружающей среды. Этот кризис объяс­няется проти­воречием между ограниченностью земных ресурсов, конечностью пригод­ных для сельскохо­зяйст­венной обработки площадей и все рас­тущими темпами потребления увеличивающегося населения. Рост насе­ления, промышленного и сельскохозяйственного производства приводит к кризису: быстрому загрязнению окру­жающей среды, истощению природных ресурсов, упадку производства и повышению смертности. На основа­нии анализа этих результатов де­лается вывод о необходимости стабилизации промышленного роста и материаль­ного по­требления.

В 80-х годах XX века появляются оригинальные работы в области глобального модели­рования в Советском Союзе. Группой ученых под руководством академика Н.Н. Моисеева в Вычисли­тельном Центре АН СССР была сделана попытка проанализировать математиче­скими мето­дами структуру международной конфликтной ситуа­ции. Основной вывод, кото­рый сле­довал из анализа составлен­ной модели, состоял в следующем. Несмотря на сложную зависи­мость целевой функции, общей для всех партнеров (функции риска ядерной войны), в дейст­виях участников конфликта, в такой сверх­сложной и сверхопасной ситуации, какой является гонка ядерных воо­ружений, существует взаимо­выгодный и эффективный компромисс.

М.м. отдельного элемента относительно проще - она может ока­заться геометриче­ским образом, функцией или ее графиком, вектором, матрицей, числовой табли­цей, скалярной величиной или даже конкретным чис­лом.

Построение мо­дели, адекватно отра­жающей объект, - дело непростое и требует специ­альных знаний и хорошей математиче­ской подготовки.

МЕТОД МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ сводит исследование внешнего мира к мате­ма­тическим задачам.

Процесс математического моделирования состоит из четырех эта­пов:

1) формализации, т. е. перехода от реальной практической задачи (исследуемой си­туа­ции) к по­строению аде­к­ватной математической модели и формулировки на ее ос­нове абст­рактной математической задачи;

2) решения задачи путем преоб­разования модели (проведение математического иссле­дования), т.е. получение в результате анализа и исследования модели выходных данных (теоретических сведений);

3) интерпретации полученного результата, когда решение формальной математи­че­ской задачи исследуется на предмет его соответствия с исходной ситуацией, истол­ковыва­ется в терминах исходной ситуации и применяется к ней;

4) модернизации модели, т.е. построение новой более совершенной модели в связи с на­коплением данных об изучаемом объекте или процессе.

Пример 4. Разработка модели Сол­нечной системы. Наблюдения звездного неба, начавшиеся еще в глубокой древности, при­вели к тому, что из всего многообразия небесных светил были выде­лены планеты, которые и стали объектом изучения. Следующим ша­гом явилось изучение закономер­ностей их дви­жений, т.е. построение моделей и получение конкретных резуль­татов. Модели Солнеч­ной системы в процессе своего развития прошли через ряд усовершенствований по мере накоп­ления экспе­риментальных данных и развития науки. Первой была модель Птолемея, создан­ная во II веке нашей эры, исходила из положения, что планеты и Солнце совершают движе­ния вокруг Земли (т.н. геоцентриче­ская модель).

В XVI веке появилась модель Н. Коперника, принципи­ально отличающаяся от предыдущей, пола­гающая, что планеты вращаются вокруг Солнца по окружности (т.н. гелиоцен­три­ческая модель). Затем появи­лась модели И. Кеплера (начало XVII века), И. Ньютона (вторая поло­вина XVII века), описывающие движения пла­нет на ма­тематическом языке. Модель Ньютона, осно­ванная на законе всемирного тяготения, вполне удовлетворительно описывала движение известных планет и давала возможность вы­чис­лять их положение на небо­своде.

Но вот к 40-м годам XIX в. не­которые результаты этой мо­дели стали тоже не согласовываться с экспе­риментальными данными: наблюдаемое движе­ние Урана уклонялось от теоретически вычисляемого движения. Французский ученый-ас­троном У. Леверье расширил систему наблюдаемых планет новой гипотетической плане­той (он на­звал ее Нептуном) и, пользуясь новой математической моделью, определил все ос­нов­ные па­раметры этой планеты. В указанное время и на предсказанном им месте в 1846 году астро­номы убедились в реальном существовании еще одной планеты Солнечной сис­темы. По­добные вычисле­ния, сделанные П. Лоуэлом, при­вели в 1930 году к открытию де­вятой пла­неты, получившей название Плутон.

В ходе многовекового исторического развития математики сконст­руированы осо­бые мо­дели количественных отношений и пространственных форм ок­ружаю­щего мира. Это такие математические понятия, как число, функция, уравнение, гео­метриче­ская фигура и др. Хотя математическая модель и создается человеческим разумом, в даль­нейшем она во многих случаях становится предметом объективного изучения. Познавая ее свойства, мы тем самым познаем и свойства отраженной моделью реаль­но­стей, т.е. абст­рактные математические открытия обнаруживают ранее неизвестные свойства окружающего мира.

Например, представле­ние, что числа бывают только, скажем, до миллиарда (а дальше чисел нет!) прямым наблюдением вряд ли может быть опро­вергнуто. Только создание мате­матиками древности такого понятия нату­рального числа (такой модели), при ко­тором нату­ральных чисел оказывалось беско­нечно много, позволяет это сделать. С помощью модели геометрии Лобачевского че­ловечество пришло к пониманию искрив­ленности пространства, абстрактные функ­циональные зависимости дают возможность пред­сказывать развитие тех или иных процессов, модели геометрических тел позволяют на прак­тике определять количе­ст­венные характеристики окружающих нас предметов и т.д.

Для исследования существующих и построения новых моделей в математике раз­рабо­таны специальные методы. Среди них методы теории графов, теории вероятно­стей и математической статистики, математической логики и комбинаторики, ак­сио­матический метод, методы иссле­дования элементарных функций, решения уравнений, доказательства утверждений, построения геометрических фигур, измерения величин и т.д. Так, идеи метода моделирования находят свое примене­ние при решении тексто­вых задач: во-первых, само понятие текстовой задачи можно ввести, пользуясь поня­тием «модель», во-вторых, понятия мо­дели позволяет строго определить понятия «метода решения» и «способа решения» тексто­вой задачи.

В математике разработаны и особые методики использования на практике матема­тиче­ских моде­лей, например, приемы решения задач с помощью уравнений и систем уравнений, изучение различных явлений и процессов с помощью исследования соот­ветствующих функ­ций, графов, геометрических фигур и т.д.

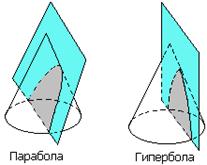
Пример 5. Общеизвестно, что, разрезая конус плоскостями, не проходящими через его вершину, мы полу­чаем в сечении различные кривые: окружности, эллипсы, параболы, гиперболы (рис. 4.7). Их называют коническими сече­ниями. Еще древнегреческие ученые начали зани­маться изучением этих кривых, т.к. они встречаются в различ­ных явлениях природы и в че­ловече­ской деятельности (в астро­номии, в во­енном деле, в физики и т.п.). Однако лишь, ко­гда поя­вились уравнения конических сечений, полу­ченные методом координат, изучение этих кри­вых значительно продвинулось вперед, и были ре­шены многие задачи, связанные с ними. Так, И. Кеплер (1609 г.) открыл из наблюдений, а И. Ньютон (1687 г.) теоретически обосно­вал, что планеты и кометы Солнечной сис­темы движутся по этим кривым.

Заметим, что уравнения x ² + y ² = r ², 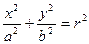, y = kx ² и  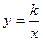выступают в каче­стве мо­делей окружности, эллипса, параболы и гиперболы, соответственно, а эти кривые в свою очередь можно рас­сматривать как геометрические модели указанных уравнений.

 

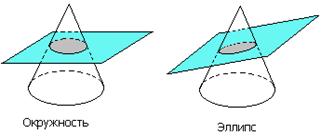Рис. 4.7

ЗНАКОВЫЕ МОДЕЛИ. Большую роль в современной науке (т.е. не только в ма­тематике) играют знаковые мо­дели. Они позволяют в виде выражений, формул, урав­нений и т.п. отображать различные процессы и существенные отношения между изу­чаемыми предметами и явлениями, с помощью термина (слова) или знака - вводить новое понятие. Например, вы­ражение a + b служит моделью суммы двух чисел; фор­мула m =2 k, где k Î N, задает четные на­туральные числа; уравнения Zn – 2e = Zn²⁺ и 2H⁺ + 2e = H₂ описывают реакции с отдачей и приемом электронов. Каждому образо­ванному человеку не составляет труда понять, что вы­ражают формулы H₂O, H₂SO₄, E = mc ², a ² + b ² = c ², S = a·b, и знаки «=», «+», «sin», «+», «g», «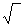», «e», «p» соответст­венно в химии, фи­зике и математике.

Часто одна и та же знаковая модель описывает различные объекты или процессы. На­пример, знаковая модель «A» может отображать точку, множество, высказывание, объект; модель «y = k·x» - зависимость между ценой, стоимостью и количеством то­вара; или между работой, производительностью труда и временем выполнения ра­боты и др. С другой сто­роны, один и тот же процесс можно описать разными моде­лями. Например, реакцию взаимо­действия цинка с уксусной кислотой в молекуляр­ном виде задают уравнением Zn + 2CH₃COOH = Zn(CH₃COO)₂ + H₂, в молекулярно-ионном – уравнением Zn+2CH₃COOH = Zn²⁺ + 2CH₃COO^– + H₂.

З.м. понятия «число». Понятие числа явля­ется одним из важнейших в математике и центральным понятием курса математики в на­чальной. Появившись в простейшем виде еще в первобытном об­ществе из потребностей счета, понятие числа совершенст­вова­лось на протяжении всего последующего развития человеческой цивилизации. В вузе сту­денты, в силу выбранной профессии, изучают большинство известных число­вых множеств, и они знают, что развитие понятия числа происходило под влиянием двух факторов: прак­тиче­ской деятельности человека и внутренних потребностей ма­тематики. В процессе обучения у них формируется представление о том, что бывают порядковые числа, ко­личественные числа, числа как меры величин и числа как ком­понент вычислений.

Однако многие из них не видят разницы между понятием числа и его названием (за­писью), для большинства из них эти понятия тождественны. На во­прос: «Какие числа называются натуральными?», - обычно следует ошибочный ответ: «1, 2, 3 и т.д. – это натуральные числа». Ответ неправильный, по­тому что студенты в данной ситуации подменяют само понятие его обозначением: 1, 2, 3 и т.д. – это не на­туральные числа, а их обозначения, их символы, их знаковые модели. Понятие числа, возникшее как ма­тематическая модель операции пересчета предметов, само стано­вится основой для построения новых математических моделей.

Системы счисления и нумерации – это способы знаково-сим­воличе­ского модели­рования натуральных чисел. Например, любое натуральное число s в десятич­ной сис­теме счисления можно представить в виде:

s = a_n 10 ⁿ + a_{n -1}10 ^{n -1} + a ₁10¹ + a ₀ = a_na_{n -1}  a ₁ a ₀, где a_i < 10, i = 0,1,2, n, a_n ≠ 0.

Числа a_i называются однозначными числами, а их обозначения (символы 1, 2, 3, 9, т.е. знаковые модели) называются цифрами. Следовательно, и запись a_na_{n -1}. a ₁ a ₀ есть знаковая модель числа s. Другими знаковыми моделями натуральных чисел яв­ляются их представле­ния цифрами римской нумерации, старославянской нумерации и др.

Большое разнообразие знаковых моделей представляют в наше распоряжение ра­цио­нальные числа, которые можно записать в виде:

а) обыкновенной дроби, например, 12/7, 2/3;

б) десятичной конечной или десятичной бесконечной периодической дроби, на­пример, 3,5; 2,(36); 12,17(3);

в) конечной непрерывной (или цепной дроби), например,

;

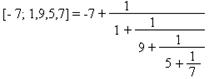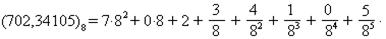
г) систематической дроби, например,

В зависимости от целей, которые стоят перед исследователем, используется та или иная знаковая модель рационального числа. Так, при проведении теоретических ис­следований предпочтении отдают непрерывным дробям, при выполнении практиче­ских вычислений – десятичным и обыкновенным, и т.д.

Универсальной моделью действительного числа является бесконечная десятичная дробь. При этом, если эта дробь периодическая, то изображаемое ею действительное число является рациональным; если же эта дробь непериодическая, то изображаемое ею действительное число является иррациональным. Другими знаковыми моделями действительных чисел яв­ляются непрерывные дроби (конечные и бесконечные), ир­рациональные числа, которые изо­бражаются с помощью знаков корней (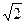, , 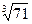 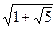и др.), трансцендентные числа (p = 3,141592, e = 2,718281 и др.).

АКСИОМАТИЧЕСКИЙ МЕТОД И МОДЕЛИРОВАНИЕ. Особая роль принад­лежит модели­рованию в установлении истинности той или иной формы теоретиче­ского знания (ак­сиоматической теории, гипотезы и т.д.). Модель здесь можно рас­сматривать как ору­дие проверки того, действительно ли существуют такие связи, от­ношения, структуры, закономерности, которые формулируются в данной теории и выполняются в модели, а ус­пешная работа модели - это практическое доказательство истинно­сти теории, т.е. это часть экспериментального доказательства истинности этой теории.

Сформулировав основные по­нятия (объекты и отношения), а так же ак­сиомы неко­торой теории, мы имеем лишь ло­ги­че­скую схему, в кото­рой все понятия счита­ются «пустыми» (не имеющими конкретный смысл). Требование только одно: данные по­ня­тия должны формально удовлетворять аксиомам. Ос­тальные свой­ства этих и новых понятий (т.е. тех, которые будут введены в дальнейшем) должны быть ло­гически вы­ведены из ак­сиом.

Придав основным объектам и отношениям аксиоматики конкретный смысл, мы по­лучим ее модель. Ценность моделей в этом случае заключается в том, что они дают возможность прове­рить логическую стройность аксиоматики. При этом, как только понятиям аксиоматики при­дан конкретный смысл, ее ак­сиомы становятся теоремами, которые уже нужно доказы­вать.

Так, моделями булевой алгебры являются алгебра множеств и ал­гебра вы­сказыва­ний, моделью числового поля – множество действительных чисел с заданными на нем операциями сложения и умножения. Интересные модели предоставляют в наше рас­поряжение аксиоматики евклидовой гео­метрии и геомет­рии Лобачевского.

Пример 6. Модель №1 евклидовой геометрии. Условимся под словами «точка», «прямая» и т.д. подразуме­вать следующее (другими словами, придадим конкретный смысл основным понятиям). «Точка» – любая точка обыкновенной плоскости, кроме одной точки O; «прямая» – окружность в широком смысле, проходящая через точку O, т.е. любая окруж­ность или прямая, проходящая через точку O (можно считать, что обыкновенная прямая – это окружность с бесконечно большим радиу­сом.); «принадлежит» – в обычном смысле. Чтобы не услож­нять пример, истолкование других слов («между», «конгруэнтен» и т.д.) приводить не бу­дем.

Можно показать, что для таких «точек» и «прямых» выпол­няются все ак­сиомы евклидо­вой гео­метрии. Например, аксиома «Через две раз­личные точки проходит одна и толь­ко одна пря­мая» ста­новится в на­шей модели теоремой «Через три точки проходит единствен­ная ок­ружность в широ­ком смысле». Дока­жем ее. Пусть «точки» B и C (рис. 4.8) таковы, что точка O не лежит на пря­мой BC.

Из планиметрии Евк­лида известно, что через три точки (B, C и O), не лежащие на одной прямой, проходит единственная окружность. Если же «точки» B и C таковы, что BC проходит через O, то B и C определяют единст­венную прямую, прохо­дя­щую через O. Что и требовалось доказать.

Пример 7. Модель №2 евклидовой геометрии. Введем словарь по­нятий. «Точка» - всякая упо­рядоченная пара чисел (х,у); «прямая» - множе­ство точек, координаты которых удовле­творяют урав­не­нию вида

Ax + By + С = 0; «при­надле­жит» - «точка» (x ₀, y ₀) лежит на «пря­мой» Ax + By + С = 0, если Ax ₀ + By ₀ + С = 0; «между» - точка B (x ₂, y ₂) лежит между A (x ₁, y ₁) и C (x ₃, y ₃), если выполняется хотя бы одно из сле­дующих отношений: x ₁< x ₂< x ₃, x ₃< x ₂< x ₁, y ₁< y ₂< y ₃ или y ₃< y ₂< y ₁; «конгруэнтен» (для отрезков) - отрезок A (x ₁, y ₁) B (x ₂, y ₂) кон­груэнтен от­резку C (x ₃, y ₃) D (x ₄, y ₄), если (x ₁- x ₂)² + (y ₁- y ₂)² = (x ₃- x ₄)² + (y ₃- y ₄)² и т.д.

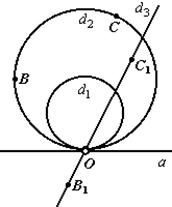
Рис. 4.8

Геометрия Лобачевского, не получившая признания при жизни ее автора, стала из­вест­ной только после того, как появилась ее первая модель.

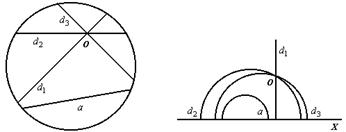
Пример 8. Модель Кели-Клейна геометрии Лобачевского. Введем словарь понятий. «Плос­кость» - фик­си­рованный круг; «точка» - обычная точка, находящаяся внутри круга, «пря­мая» - хорда окружнос­ти (без концов); «лежать», «между» – в обычном смысле. Чтобы не усложнять пример, истолкование дру­гих слов приводить не будем.

Можно показать, что на этой модели выполняются все аксиомы геометрии Евклида кроме ак­сиомы IV о па­раллельных. Вместо нее выполняется аксиома Лобачевского: «Через точку вне прямой проходит более одной прямой, не пересекающей данную». На рис 9а через точку O проходят три «прямые» d ₁, d ₂ и d ₃, параллельные «прямой» a.

Пример 9. Модель Пуанкаре геометрии Лобачевского. Введем словарь понятий. «Точка» - обыч­ная точка, находящаяся в верхней полуплоскости (x >0), «пря­мая» - луч, перпендику­лярный оси X, а также полуокружности, опирающиеся на ось X (см. рис. 9б); «лежать», «между» – в обычном смысле. Чтобы не усложнять пример, ис­толкование других слов при­водить не будем. На рис. 9б через точку O проходят три «прямые» d ₁, d ₂ и d ₃, парал­лельные «прямой» a.

Наличие моделей доказывает, что сис­тема ак­сиом Лобачевского является непро­тиворечивой.

Построение моделей геометрий Евклида и Лобачевского позволило решить про­блему 2000-летней дав­ности: можно ли доказать аксиому о параллельных, т.е. вы­вести ее из дру­гих аксиом? Те­перь ясно, что нельзя, потому что эта аксиома не зави­сит от остальных ак­сиом. Независи­мость вытекает из того факта, что после замены аксио­мы параллельности Евклида на ак­сиому параллельности Лобачевского мы вновь получаем непротиворечивую си­стему аксиом.

Открытие неевклидовой геометрии показывает, что появление новых математиче­ских мо­делей нередко означает не только принципиальный поворот в развитии самой математики, но и меняет существующие знания об окружающем нас мире.

МОДЕЛИ В ОБУЧЕНИИ. Модели помимо всего прочего являются тем учебным средством, без кото­рого невоз­можно полно­цен­ное обучение. На уроках математике в начальной школе находят применение как материальные, так и идеальные модели. К ним относятся, например, наглядные пособия, которые воспроизводят реальные и идеальные объекты, передают их структуру, существенные свойства, связи и от­ноше­ния, допуская при этом уменьшение или увеличение раз­мера, схематическое изобра­же­ние. По способу предъявления учащимся такие модели делятся на демонстрацион­ные и раз­даточные (индивидуальные).