Среди процессов, происходящих с газами, часто встречается и очень важен адиабатический процесс, протекающий без передачи тепла. Чтобы получить его уравнение, воспользуемся первым началом термодинамики. Его формулировка: теплота, сообщаемая системе (газу), идет на изменение внутренней энергии системы и на совершение системой работы над внешними силами (против действия внешних сил)
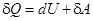 .
.
Для записи передаваемого тепла удобно ввести понятие теплоемкости 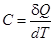 - это величина, равная количеству теплоты, которую надо сообщить системе, чтобы повысить ее температуру на 1 К. Далее этим символом будем обозначать молярную теплоемкость, относящуюся к 1 молю вещества.
- это величина, равная количеству теплоты, которую надо сообщить системе, чтобы повысить ее температуру на 1 К. Далее этим символом будем обозначать молярную теплоемкость, относящуюся к 1 молю вещества.
Величина теплоемкости зависит от способа, которым системе сообщается тепло. Процессы с постоянной теплоемкостью называются политропическими. Одним из таких процессов является процесс нагревания идеального газа при постоянном объеме (изохорический процесс). Молярная теплоемкость такого процесса обозначается 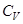 .
.
Так как работа, совершаемая газом при увеличении его объема на dV равна 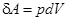 , то при изохорическом процессе работа газом не совершается, т.е.
, то при изохорическом процессе работа газом не совершается, т.е. 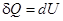 и
и
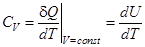 .
.
Отсюда, изменение внутренней энергии одного моля идеального газа будет 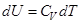 , а для произвольной массы m газа
, а для произвольной массы m газа 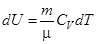 .
.
Тогда первое начало термодинамики для идеального газа можно записать в виде:
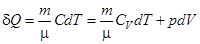 . (1)
. (1)
Процесс, протекающий при постоянном давлении, называется изобарическим, а молярная теплоемкость для такого процесса обозначается СР . Найдем связь между теплоемкостями для упомянутых процессов. Для этого нам понадобится уравнение состояния для одного моля идеального газа
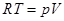 , (2)
, (2)
где R - универсальная газовая постоянная. Отсюда, при p=const, находим, что 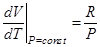 , а из уравнения (1) имеем
, а из уравнения (1) имеем
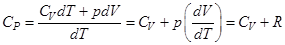 . (3)
. (3)
Эта связь молярных теплоемкостей называется уравнением Майера.
Теперь рассмотрим адиабатический процесс, для которого 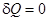 , и первое начало термодинамики (1) для одного моля идеального газа запишется в виде:
, и первое начало термодинамики (1) для одного моля идеального газа запишется в виде:
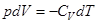 . (4)
. (4)
В уравнении состояния (2) для одного моля идеального газа меняются все термодинамические параметры, p, V, и T. Вычисляя дифференциал, получим 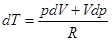 . Подставляя это выражение в уравнение (4), находим, что
. Подставляя это выражение в уравнение (4), находим, что 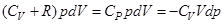 .
.
Отношение 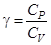 называется показателем адиабаты. В последнем полученном уравнении разделим переменные и проинтегрируем:
называется показателем адиабаты. В последнем полученном уравнении разделим переменные и проинтегрируем: 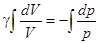 .
.
Отсюда 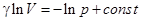 . Отсюда получаем уравнение адиабатического процесса для идеального газа или уравнение Пуассона:
. Отсюда получаем уравнение адиабатического процесса для идеального газа или уравнение Пуассона: 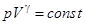 . (5)
. (5)
Используя уравнение состояния (2) можно записать уравнение Пуассона через другие термодинамические переменные: 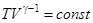 или
или 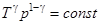 . (6)
. (6)
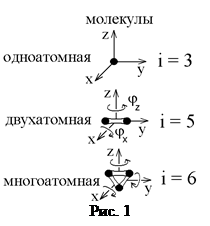 Идеальный газ – это совокупность не взаимодействующих друг с другом на расстоянии молекул. Такие молекулы к тому же не деформируются, т.е. имеют постоянную форму и очень малый размер. Размером одноатомной молекулы вообще пренебрегают, считая ее материальной точкой, способной двигаться в трех независимых направлениях, т.е. имеющей i = 3 степени свободы. Двухатомные и многоатомные молекулы имеют дополнительные вращательные степени свободы, показанные на рис. 1.
Идеальный газ – это совокупность не взаимодействующих друг с другом на расстоянии молекул. Такие молекулы к тому же не деформируются, т.е. имеют постоянную форму и очень малый размер. Размером одноатомной молекулы вообще пренебрегают, считая ее материальной точкой, способной двигаться в трех независимых направлениях, т.е. имеющей i = 3 степени свободы. Двухатомные и многоатомные молекулы имеют дополнительные вращательные степени свободы, показанные на рис. 1.
Внутренняя энергия идеального газа складывается только из кинетической энергии его молекул. Скорости молекул такого газа различны, но подчиняются распределению Максвелла. С его помощью можно вычислить среднюю энергию, приходящуюся на 1 степень свободы молекулы: 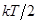 , где
, где 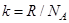 - постоянная Больцмана, R - универсальная газовая постоянная,
- постоянная Больцмана, R - универсальная газовая постоянная, 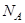 - число Авогадро. Тогда средняя энергия одной молекулы с i степенями свободы равна
- число Авогадро. Тогда средняя энергия одной молекулы с i степенями свободы равна 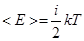 , а так как 1 моль газа содержит
, а так как 1 моль газа содержит 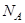 молекул, то его внутренняя энергия
молекул, то его внутренняя энергия 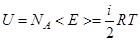 .
.
Сравнивая с термодинамической формулой 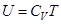 , находим, что идеальный газ из молекул с i степенями свободы имеет молярные теплоемкости
, находим, что идеальный газ из молекул с i степенями свободы имеет молярные теплоемкости 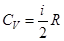 ;
; 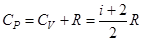 , и показатель адиабаты
, и показатель адиабаты
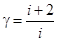 . (7)
. (7)
Для одноатомного газа 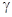 =1,667, для двухатомного -
=1,667, для двухатомного - 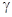 =1,40, для многоатомного -
=1,40, для многоатомного - 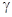 = 1,333.
= 1,333.
Воздух является смесью многих газов - двухатомных N 2 , O 2 ,…, трехатомных - СО 2, Н 2 О и т.п. Так как доля многоатомных и одноатомных газов в нем мала, то можно ожидать, что величина 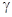 для воздуха будет близка к соответствующему значению для двухатомных газов:
для воздуха будет близка к соответствующему значению для двухатомных газов: 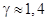 .
.
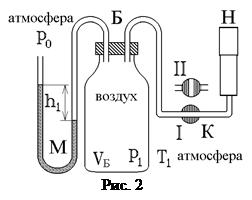 Для экспериментального определения показателя адиабаты воздуха используется установка, изображенная на рис.2. Она состоит из большого стеклянного баллона Б, соединенного через кран К с насосом Н или атмосферой. Манометр М служит для измерения разностей давлений газа в баллоне и в атмосфере. В условиях эксперимента воздух можно считать идеальным газом.
Для экспериментального определения показателя адиабаты воздуха используется установка, изображенная на рис.2. Она состоит из большого стеклянного баллона Б, соединенного через кран К с насосом Н или атмосферой. Манометр М служит для измерения разностей давлений газа в баллоне и в атмосфере. В условиях эксперимента воздух можно считать идеальным газом.
Повернем кран К в положение I, соединяя баллон с насосом, и начнем накачивать воздух в баллон. Так как этот процесс происходит достаточно медленно, то за счет теплообмена через стеклянные стенки баллона успевает установиться тепловое равновесие. Температура воздуха внутри баллона после накачивания будет равна комнатной температуре Т1 . Но давление внутри возрастет до величины
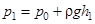 , (8)
, (8)
где p0 - давление воздуха в окружающей атмосфере, а 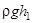 - разность гидростатических давлений жидкости с плотностью
- разность гидростатических давлений жидкости с плотностью 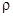 в левой и правой трубках U - образного манометра (рис. 2).
в левой и правой трубках U - образного манометра (рис. 2).
Вытащим теперь трубку крана К, соединяя баллон с атмосферой. Воздух очень быстро выходит через отверстие, расширяясь, теплообмен не успевает произойти и процесс можно считать адиабатическим. В соответствии с уравнением (3-6) при резком уменьшении давления уменьшится и температура: воздух в баллоне будет охлажден до температуры ниже комнатной!
В момент, когда давление воздуха в сосуде сравнивается с атмосферным (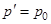 , выравниваются уровни жидкости в манометре), пробка крана плотно закрывает баллон в положении II (рис. 2). За счет теплообмена через стенки закрытого баллона начинается изохорическое нагревание охлажденного воздуха в нем. При этом давление в баллоне растет и уровни жидкости в манометре постепенно расходятся до тех пор, пока температура внутри баллона не станет равной комнатной: Т2 = Т1 . В этот момент давление воздуха в баллоне установится на величине
, выравниваются уровни жидкости в манометре), пробка крана плотно закрывает баллон в положении II (рис. 2). За счет теплообмена через стенки закрытого баллона начинается изохорическое нагревание охлажденного воздуха в нем. При этом давление в баллоне растет и уровни жидкости в манометре постепенно расходятся до тех пор, пока температура внутри баллона не станет равной комнатной: Т2 = Т1 . В этот момент давление воздуха в баллоне установится на величине
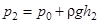 . (9)
. (9)
Процессы, протекающие в системе, изображены на рис. 3. В момент окончания адиабатного расширения в баллоне останется часть воздуха с массой m1 , занимавшая первоначально объем V1, меньший объема баллона V Б .
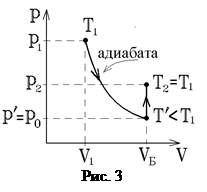 Запишем для этой части уравнения адиабатического (6) и изохорического процессов:
Запишем для этой части уравнения адиабатического (6) и изохорического процессов:
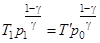 и
и
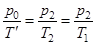 , а затем устраним неизвестное отношение температур:
, а затем устраним неизвестное отношение температур:
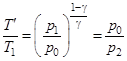 . (10)
. (10)
Логарифмируя последнее уравнение (10), получим
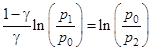 , откуда
, откуда 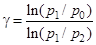 . (11)
. (11)
Подставляем сюда формулы (8) и (9):
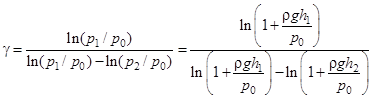 . (12)
. (12)
Но уровни жидкости (воды с плотностью 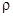 = 1000 кг/м3) раздвигаются в манометре М на рис. 2 всего на
= 1000 кг/м3) раздвигаются в манометре М на рис. 2 всего на 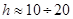 см, и избыточное давление газа
см, и избыточное давление газа 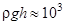 Па много меньше атмосферного давления
Па много меньше атмосферного давления 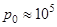 Па. Поэтому величина
Па. Поэтому величина 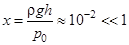 , и в формуле (12) можно разложить все логарифмы в ряд, оставляя слагаемые только первого порядка малости:
, и в формуле (12) можно разложить все логарифмы в ряд, оставляя слагаемые только первого порядка малости: 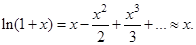 Тогда из формулы (12) получаем конечную формулу для вычисления показателя адиабаты:
Тогда из формулы (12) получаем конечную формулу для вычисления показателя адиабаты:
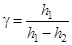 . (13)
. (13)
Такой показатель позволяет описать многие свойства исследуемого газа, но точность его определения в данном эксперименте не слишком высока, и поэтому возникают отклонения от теоретически ожидаемого значения 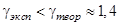 . Это связано не только с тем, что свойства реального воздуха немного отличаются от свойств идеального газа и состоит он не только из двухатомных молекул, но, главным образом - с несовершенством используемого оборудования. При установке пробки крана К в положение II (рис.2) остаются крохотные щели, и воздух понемногу продолжает вытекать из баллона при нагревании. Поэтому уровень h2 оказывается немного меньшим того уровня, который установился бы при идеально закрытом баллоне. Величина
. Это связано не только с тем, что свойства реального воздуха немного отличаются от свойств идеального газа и состоит он не только из двухатомных молекул, но, главным образом - с несовершенством используемого оборудования. При установке пробки крана К в положение II (рис.2) остаются крохотные щели, и воздух понемногу продолжает вытекать из баллона при нагревании. Поэтому уровень h2 оказывается немного меньшим того уровня, который установился бы при идеально закрытом баллоне. Величина 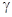 , измеренная в такой установке, в соответствии с формулой (13) тоже окажется немного меньшей, чем истинная.
, измеренная в такой установке, в соответствии с формулой (13) тоже окажется немного меньшей, чем истинная.
Оборудование: стеклянный баллон, кран, насос, манометр.
Рабочее задание: рассчитать показатель адиабаты воздуха.
 2015-04-06
2015-04-06 544
544








