Практическая работа. Задания: Вычислить приближенное значение определенного интеграла от заданной функции (см

Задания:

1. Вычислить приближенное значение определенного интеграла 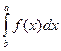от заданной функции (см. таблицу 1) по обобщенной формуле трапеций, если число частичных отрезков задано: n=20 (составить программу). Оценить погрешность вычислений, пользуясь формулой остаточного члена.
2. Вычислить этот же интеграл по формуле средних прямоугольников. Оценить погрешность вычислений. Сравнить точность полученных по разным формулам результатов.
3. Вычислить определенный интеграл 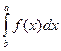от заданной функции (см. таблицу 2) с точностью до e=10^-6 по общей формуле Симпсона (составить программу с использованием формулы двойного пересчета).

Данные к заданию 1-2(таблица 1):

№	f(x)	a	b
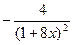
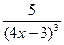
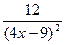
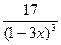
		-3	-1
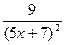
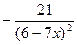
		-2
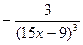
		-1

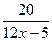
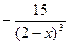
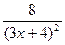
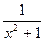
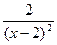
Данные к заданию 3 (таблица 2):

№	f(x)	a	b
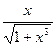
		0.8	1.8
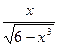
		0.8	1.8
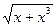
		0.6	1.6
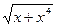
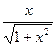
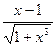
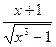
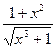
		1.3
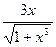
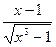
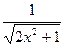
		0.8	2.8

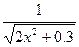
Контрольные вопросы:

1. Понятие определенного интеграла.
2. В чем заключается принцип двойного пересчета?
3. Геометрический смысл квадратурных формул?
4. Оценка точности квадратурных формул?
5. Формулы трапеции и прямоугольников.
6. Формула Симпсона.