Методы численного интегрирования

Пусть на отрезке 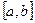задана функция 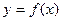. С помощью точек 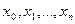разобьем отрезок 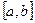на n элементарных отрезков 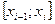(i=1,2,...,n), причем 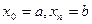. На каждом из этих отрезков выберем произвольную точку 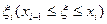и найдем произведение 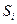значения функции в этой точке 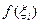на длину элементарного отрезка :

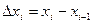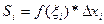
Составим сумму всех таких произведений:

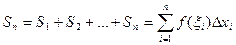
Сумма 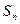называется интегральной суммой. Определенным интегралом от функции 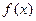на отрезке 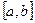называется предел интегральной суммы при неограниченном увеличении числа точек разбиения, при этом длина наибольшего из элементарных отрезков стремится к нулю:

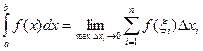
Во многих случаях, когда подынтегральная функция задана в аналитическом виде, определенный интеграл удается вычислить непосредственно по формуле Ньютона-Лейбница. Однако на практике этой формулой не всегда можно воспользоваться по двум основным причинам: 1) вид функции 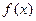не допускает непосредственного интегрирования, т. е. первообразную нельзя выразить в элементарных функциях; 2) значения функции 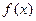заданы только на фиксированном конечном множестве точек 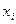, т.е функция задана в виде таблицы. В этих случаях используются методы численного интегрирования.

Приведем ряд формул численного интегрирования:

1. Формула средних прямоугольников:

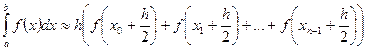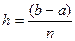, где - шаг.

Остаточный член:

.

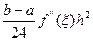2. Формула трапеций:

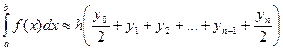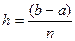, где - шаг.

Остаточный член:

.

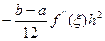3. Формула Симпсона:

,

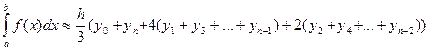где 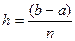- шаг.

Остаточный член:

.

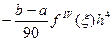Двойной пересчет по формуле Симпсона заключается в следующем: первоначально отрезок 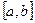разбивается на 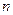частей с шагом 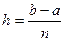. Вычисляется значение интеграла 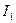. Потом число отрезков удваивается, вычисляется значение интеграла 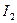с шагом 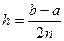, т.е. предыдущий шаг делится пополам. Условие окончания счёта принимается в виде 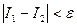. Если это условие не выполнено, происходит новое деление шага пополам и т.д.