1) Все n наблюдений упорядочиваются по величине X2 и X3.
Таблица 8.4.1 – Упорядоченные значения по фактору х2
| № п/п | 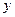
| 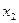
|
| 0,4 | ||
| 0,7 | 0,4 | |
| 2,2 | 0,5 | |
| 2,4 | 0,9 | |
| 3,3 | 1,3 | |
| 2,9 | 1,6 | |
| 2,3 | 1,6 | |
| 2,5 | 1,9 | |
| 2,9 | 2,2 | |
| 2,9 | 2,4 | |
| 3,6 | 3,2 | |
| 3,5 | 3,3 | |
| 3,4 | ||
| 3,5 | ||
| 3,4 | 3,6 | |
| 3,5 | 3,7 | |
| 3,3 | 3,8 | |
| 2,7 | 4,2 | |
| 2,3 | 5,1 | |
| 3,5 | 5,3 | |
| 2,5 | 5,3 | |
| 3,2 | 5,6 | |
| 4,2 | 6,1 | |
| 8,5 | 16,8 | |
| 5,7 | 27,5 |
Таблица 8.4.2 – Упорядоченные значения по фактору х3
| № п/п | 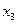
| 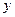
|
| 1,6 | ||
| 8,9 | 2,2 | |
| 9,2 | 2,3 | |
| 10,3 | 2,9 | |
| 12,9 | 2,4 | |
| 16,4 | 3,5 | |
| 16,5 | 2,5 |
Продолжение таблицы 8.4.2
| 19,3 | 3,3 | |
| 22,8 | 3,5 | |
| 23,8 | 3,5 | |
| 24,9 | 3,3 | |
| 25,2 | 3,6 | |
| 27,2 | 2,9 | |
| 31,1 | 2,3 | |
| 32,9 | 3,2 | |
| 36,9 | 2,5 | |
| 37,2 | 2,9 | |
| 40,4 | ||
| 40,8 | 4,2 | |
| 50,4 | 0,7 | |
| 53,8 | 2,7 | |
| 54,6 | 3,4 | |
| 81,5 | ||
| 133,5 | 5,7 | |
| 286,5 | 8,5 |
2) Исключим С центральных наблюдений, разобьем совокупность на две части: а) со значениями x ниже центральных; б) со значениями x выше центральных.
Пусть С=5, это наблюдения с порядковыми номерами 11-15.
3) Оцениваются отдельные регрессии для первой подвыборки (10 первых наблюдений) и для третьей подвыборки (10 последних наблюдений). Если предположение о пропорциональности дисперсий отклонений значениям X верно, то дисперсия регрессии по первой подвыборке (сумма квадратов отклонений 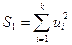 ) будет существенно меньше дисперсии регрессии по третьей подвыборке (суммы квадратов отклонений
) будет существенно меньше дисперсии регрессии по третьей подвыборке (суммы квадратов отклонений 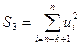 ).
).
4) По каждой части находим уравнение регрессии (рисунок 8.4.5)
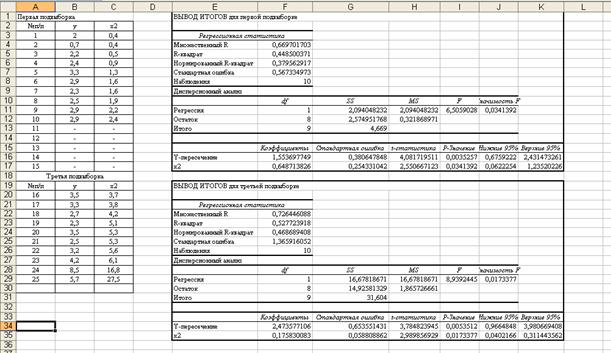
Рисунок 8.4.5 – Вывод итогов для подвыборок для фактора х2
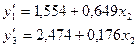
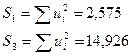
5) Для сравнения соответствующих дисперсий строится следующая F-статистика: 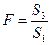
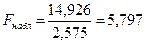
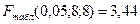
При сделанных предположениях относительно случайных отклонений построенная F-статистика имеет распределение Фишера с числами степеней свободы v1=v2=(n-C-2m)/2.
6) Если 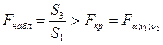 , то гипотеза об отсутствии гетероскедастичности отклоняется (
, то гипотеза об отсутствии гетероскедастичности отклоняется (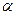 - выбранный уровень значимости).
- выбранный уровень значимости).
По проведенным расчетам мы получили, что 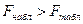 следовательно в ряду остатков обнаружена гетероскедастичность.
следовательно в ряду остатков обнаружена гетероскедастичность.
Аналогично проводится анализ для фактора х3.
 2015-04-06
2015-04-06 611
611








