Основные информационные характеристики

Пусть 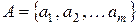- ансамбль сообщений, 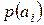- вероятность 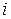-го сообщения.

Количество собственной информации в сообщении 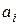определяется выражением

.

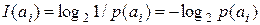(1.1)

Условная информация сообщения 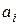при известном :

.

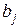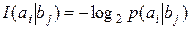(1.2)

Взаимная информация двух сообщени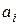й и :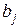

,

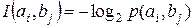(1.3)

где .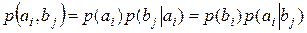

Безусловная энтропия сообщения:

.

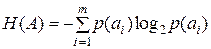(1.4)

Условная энтропия сообщения ансамбля 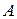относительно :

.

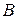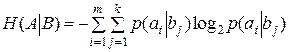(1.5)

Совместная энтропия двух ансамбле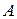й и :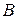

.

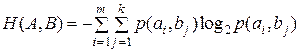(1.6)

Избыточность источника без памяти:

.

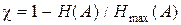(1.7)

Избыточность источника с памятью:

.

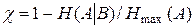(1.8)

Производительность дискретного источника сообщений:

,

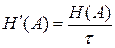(1.9)

где 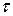- время передачи одного символа.

Скорость передачи информации по дискретному каналу (информационная скорость) для неравновероятных взаимно независимых символов, имеющих одинаковую длительность:

,

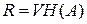(1.10)

где 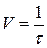- скорость передачи символов (техническая скорость).

Скорость передачи информации для равновероятных взаимно независимых символов, имеющих одинаковую длительность:

.

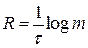(1.11)

Скорость передачи информации для взаимно независимых символов, имеющих разную длительность:

.

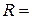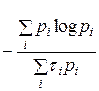(1.12)

Скорость передачи информации для взаимно зависимых символов, имеющих разную длительность:

.

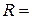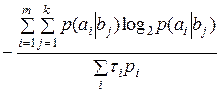(1.13)

Пропускная способность канала связи 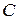, бит/симв:

.

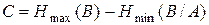(1.14)

Пропускная способность канала связи 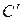, бит/сек:

.

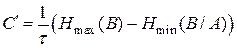(1.15)

Пропускная способность как зависимость от физических характеристик канала связи:

,

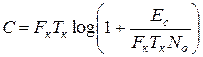(1.16)

где 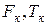- полоса частот и время передачи по каналу связи;

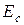- энергия сигнала;

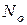- плотность мощности шума.