Правило формирования проверочных элементов

Пусть задана порождающая матрица линейного кода

.

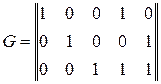Обозначим элементы кодовой комбинации кода 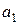, , 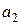, , 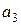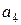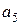. Так как в качестве информационной подматрицы берется единичная матрица, то элементы 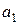- 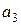являются информационными, а 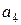, 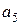- проверочными. Проверочные элементы могут быть получены путем суммирования по модулю два определенных информационных элементов. Таким образом,

;

.

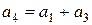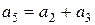Правило получения проверочной матрицы линейного кода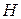

1. Число столбцов матрицы 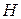равно длине кода 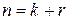, а число строк – количеству проверочных символов .

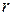2. Матрица 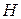состоит из двух матриц: матрицы 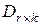, транспонированной по отношению к С 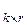, и единичной матрицы размерности ().

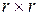3. Единицы, расположенные на местах, соответствующих информационным элементам матрицы 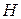, указывают на то, какие информационные элементы должны участвовать в формировании проверочного элемента. Единица на месте, соответствующем проверочному элементу, указывает на то, какой проверочный элемент получается при суммировании по модулю два информационных элементов.

Матрицы 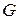и 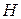должны быть взаимно ортогональны, т.е. .

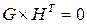Вычисление синдрома :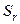

.

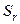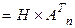(3.9)