Пример 1. Задан закон распределения дискретной случайной величены Х:
| Х | – 4 | – 2 | |||||
| р | 0,05 | р | 0,12 | 0,23 | 0,32 | 0,14 | 0,04 |
Найти:
а) неизвестную вероятность р;
б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение 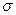 данной случайной величены;
данной случайной величены;
в) функцию распределения F(x) и построить ее график.
Решение:
а) так как сумма всех вероятностей должна равняться единице, то получим уравнение 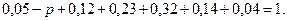 Отсюда
Отсюда 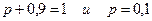
б) Математическое ожидание М это сумма всех произведений значений случайной величины на их вероятности:
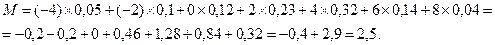
Дисперсия D= 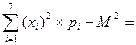
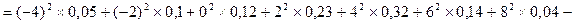
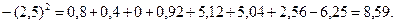
Среднее квадратическое отклонение 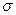 =
= 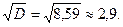
в) Если 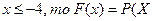 <
< 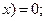
Если – 4< 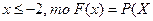 <
< 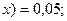
Если – 2< 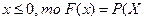 <
< 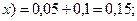
Если 0< 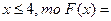 0,05 + 0,1 + 0,12 = 0,15 + 0,12 = 0,27
0,05 + 0,1 + 0,12 = 0,15 + 0,12 = 0,27
Если 2< 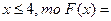 0,27 + 0,23 = 0,5;
0,27 + 0,23 = 0,5;
Если 4< 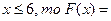 0,5 + 0,32 = 0,82;
0,5 + 0,32 = 0,82;
Если 6< 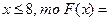 0,82 + 0,14=0,96;
0,82 + 0,14=0,96;
Если х >8, то F(x)=Р(Х < х)= 0,96 + 0,04=1.
Итак, функция распределения может быть записана так:
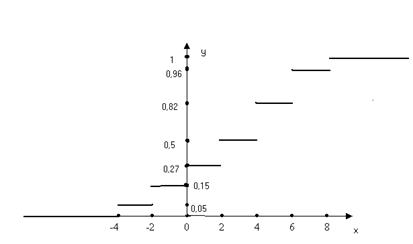 |
F (x) =
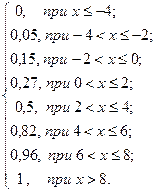
График этой функции приведен на рисунке:
 2015-04-06
2015-04-06 506
506








