2015-04-06
2217
Неявно заданная алгебраическая кривая описывается уравнением
F (x, y) = 0,
где левая часть представляет собой многочлен относительно переменных x и y.
В дифференциальной геометрии используется следующий метод нахождения наклонной асимптоты алгебраической кривой. Пусть асимптота описывается уравнением y = kx + b. Подставляя это выражение для y в уравнение кривой, получаем алгебраическое уравнение относительно одной переменной x:
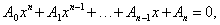
где коэффициенты Ai зависят от параметров асимптоты k и b (причем коэффициент A 0 зависит лишь от k). Значения k и b определяются из условия:
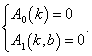
Для нахождения вертикальной асимптоты нужно подставить ее уравнение x = a в уравнение кривой и преобразовать последнее к виду:
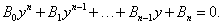
Необходимым условием существования вертикальной асимптоты является отсутствие в последнем уравнении старшего члена B 0 yn. Значение параметра a определяется из условия
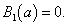
Приведенные формулы для асимптот неявно заданных кривых справедливы, если кривая не имеет особых точек на бесконечности.
