Прохождение практики осуществляется студентом в соответствии с индивидуальным заданием, указанном в методических указаниях, выдаваемом руководителем практики от кафедры. Руководитель практики от кафедры отображает итоги прохождения практики в следующих документах:
- рецензии на отчет студента по практике;
- студенческой аттестационной книжке;
- зачетной ведомости;
- зачетной книжке.
Отчет является основным документом, характеризующим работу студента во время практики. В отчете должны быть отражены изученные во время практики общие вопросы и основные результаты практической деятельности студента в соответствии с рабочей программой практики и индивидуальным заданием, полученным студентом.
Отчет долен содержать:
1. Титульный лист;
2. Перечень и содержание выполненных работ (в соответствии с заданием) и индивидуальным планом.
3. Необходимы расчеты и пояснения к индивидуальному заданию.
Отчет по практике оформляется на листах формата А4 (210×297). Отчет должен быть набран на компьютере, используя шрифт типа Times New Roman, размер шрифта – 14, межстрочный интервал – 1,5 строки. Форматирование текста – по ширине, поля стандартные (левое – 2,5см, правое – 1,5см, верхнее и нижнее – 2см) Примерный объем отчета – 20-25 страниц машинописного текста.
Отчет должен сопровождаться необходимыми расчетами, таблицами и графиками.
ПРИЛОЖЕНИЕ
Аппроксимация функций.
Применение интерполяции позволяет получить функцию, совпадающую в узлах интерполяции с имеющимися эмпирическими данными, но часто такое совпадение может не означать совпадение характеров поведения исходной и интерполирующей функций на всем интервале наблюдения (например, из-за отклонений измеренных значений функции, ввиду погрешностей измерительной аппаратуры (сами значения являются приближенными) или влияния случайных факторов на процесс измерений).
Формулировка задачи аппроксимации выглядит следующим образом.
Пусть в результате измерений в процессе опыта получено табличное задание функции 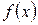 , тогда необходимо найти функцию заданного вида
, тогда необходимо найти функцию заданного вида 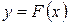 , которая в точках
, которая в точках 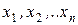 принимает значения, как можно более близкие к табличным
принимает значения, как можно более близкие к табличным 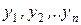 . При такой формулировке задача аппроксимации функции одной переменной учитывает характер поведения функции на интервале наблюдений.
. При такой формулировке задача аппроксимации функции одной переменной учитывает характер поведения функции на интервале наблюдений.
Практически вид приближающей функции чаще всего определяют путем сравнения приближенно построенного графика функции с графиками известных исследователю функций, заданных аналитически (как правило, элементарных функций) (рис.6).
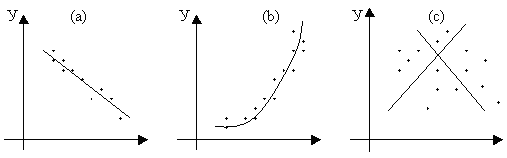
Рис. 6
На рисунке 6 изображены три ситуации:
А) взаимосвязь  и
и 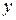 близка к линейной, прямая близка к точкам наблюдений, а последние отклоняются из-за небольших случайных воздействий;
близка к линейной, прямая близка к точкам наблюдений, а последние отклоняются из-за небольших случайных воздействий;
Б) взаимосвязь величин  и
и 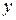 описывается нелинейной функцией, достаточно хорошо которую описывает ветка параболы;
описывается нелинейной функцией, достаточно хорошо которую описывает ветка параболы;
В) явная взаимосвязь между переменными отсутствует, отклонение любой линии от точек будет велико.
Аппроксимация позволяет находить значения функции 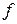 для не табличных значений
для не табличных значений  , «сглаживая» результаты измерений величины
, «сглаживая» результаты измерений величины 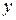 .
.
Аппроксимация методом наименьших квадратов.
При данном методе в качестве критерия близости приближающей функции 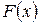 к исходной функции
к исходной функции 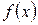 используется минимум суммы квадратов разностей наблюдений зависимой переменной
используется минимум суммы квадратов разностей наблюдений зависимой переменной 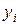 и теоретических, рассчитанных по уравнению регрессии значений
и теоретических, рассчитанных по уравнению регрессии значений 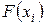 :
: 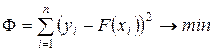 .
.
Рассмотрим метод нахождения приближающей функции в общем виде на примере аппроксимирующей функции с тремя параметрами:
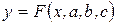 (10)
(10)
Сумма квадратов разностей соответствующих значений имеет вид:
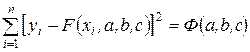
Задача сводится к отысканию минимума функции трех переменных 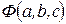 . Условие экстремума функции
. Условие экстремума функции 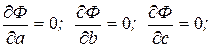
Система уравнений для определения неизвестных параметров 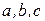 имеет вид:
имеет вид:
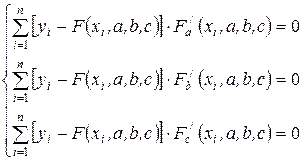 (11)
(11)
Нахождение аппроксимирующей функции в виде основных элементарных функций.
А) линейная регрессия
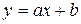
Найдем частные производные: 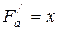 ,
, 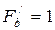
Система уравнений имеет вид:
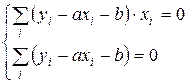
После преобразований и введения обозначений система уравнений приобретает вид:
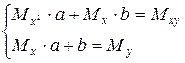
Где 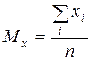 ,
, 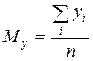 ,
, 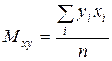 ,
, 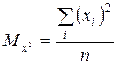
Решив данную систему, получим значения параметров 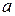 и
и 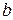
 2015-04-06
2015-04-06 1048
1048
