2015-04-06
996
линейной функции Ф = x1 + 3·x2 + 3·x3
при ограничениях: x2 + х3 ≤ 3;
х1 - х2 ≥ 0;
x2 ≥ 1;
3·x1 + x2 ≤ 15;
х j ≥ 0 (j=1, 3).
******************* РЕШЕНИЕ ********************************
Заменив в системе ограничений условно знаки неравенств знаками равенств, получим систему уравнений
x2 + х3 = 3 (1)
х1 - х2 = 0 (2)
x2 = 1 (3)
3·x1 + x2 = 15 (4)
По полученным уравнениям построим плоскости в системе координат х1 О х2 х3, то есть в трехмерном пространстве. Затем согласно знакам неравенств в системе ограничений выделим соответствующие полуплоскости, которые, пересекаясь, образуют общую часть, из которой с учетом условий неотрицательности переменных выделим область допустимых решений (ОДР) - многогранник – многогранник MSRQPN.
Из начала координат построим вектор-градиент
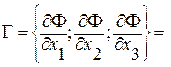(1; 3; 3)
Затем через начало координат построим плоскость уровня Фо ┴ Г, соответствующую значению целевой функции Фо = 0.
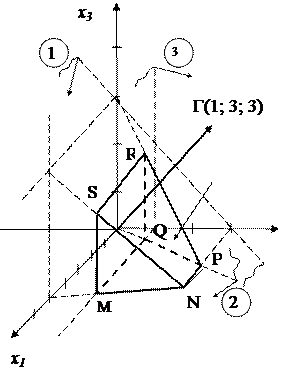Так как плоскость уровня ФоÏОДР, перемещаем ее в направлении к ОДР. Так как направление перемещения плоскости Ф совпадает с положительным направлением вектора Г, то значение целевой функции при этом возрастает. И в точке Q(1; 1; 0) плоскость уровня Ф впервые встречается с ОДР и становится опорной.
|
|
|
|
Двигаем линию плоскость Ф дальше в том же направлении (в положительном направлении Г), при этом значение целевой функции продолжает расти. В точке N (4; 3; 0) линия уровня в последний раз встречается с ОДР. В этой точке функция Ф достигает наибольшего значения, (удовлетворяющего системе ограничений), то есть Фр= maxФ = 4 + 3·3 + 3·0 = 13.
Ответ: minФ = 4 при ХQ = (1, 1, 0),
maxФ = 13 при ХN = (4; 3; 0).
