Теоретическая поддержка. Сущность транспортной задачи линейного программирования состоит в наивыгоднейшем прикреплении поставщиков однородного продукта ко многим потребителям этого

Сущность транспортной задачи линейного программирования состоит в наивыгоднейшем прикреплении поставщиков однородного продукта ко многим потребителям этого продукта. На практике постоянно возникает необходимость решения таких задач, особенно когда количество пунктов отправления и получения грузов увеличивается.

Модель транспортной задачи линейного программирования может использоваться для планирования ряда операций, не связанных с перевозкой грузов. Так, с ее помощью решаются задачи по оптимизации размещения производства, топливно-энергетического баланса, планов загрузки оборудования, распределения сельскохозяйственных культур по участкам различного плодородия и т.п.

В торговле модель транспортной задачи линейного программирования применяется для решения следующих задач: планирование товароснабжения города, района; прикрепление торговых предприятий к поставщикам; организация рациональных перевозок товаров из пунктов отправления (баз, станций, фабрик, совхо­зов, заводов) в пункты назначения (магазины, склады); распределение работников торговли по должностям (задача о назначении); планирование капиталовложений; оптимизация межотраслевых свя­зей торговли; размещение розничной торговой сети города и т.д.

Условие транспортной задачи обычно записывается в виде матрицы, в которой потребители однородного груза размещаются по столбцам, а поставщики – по строкам. В последнем столбце матрицы проставляют запас груза, имеющийся у каждого поставщика, а в последней строке – потребность в нем потребителей. На пересечении строк со столбцами (в клетках матрицы) записывают размер поставки, а также расстояние пробега по всем возможным маршрутам, время доставки груза или затраты на перевозку единицы груза по этим маршрутам.

Экономико-математическая формулировка и модель транспорт­ной задачи имеют следующий вид.

Найти такие неотрицательные значения x_ij > 0, 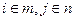, которые минимизируют затраты на перевозку грузов:

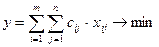
при ограничениях

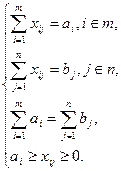
Первые уравнения представляют собой условие, что от каждого поставщика вывозится весь продукт.

Вторая группа n равенств выражает условие, что спрос каждого потребителя полностью удовлетворяется.

Третий тип ограничений связан с возможностью решения задачи при наличии баланса между предложением и спросом: 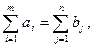что отражает сущность так называемой закрытой модели тран­спортной задачи.

Если спрос не равен предложению: 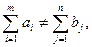то имеем открытую модель транспортной задачи, которая бывает двух видов:

а) когда предложение больше спроса, т. е. 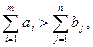вводят «фиктивного» потребителя с заявкой 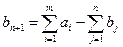и транспортными издержками .

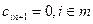При решении задачи часть товаров попадает к фиктивному потре­бителю, а фактически это означает, что этот груз останется на соот­ветствующей базе поставщика;

б) когда предложение меньше спроса, т. е. 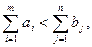при распределении продукции руководствуются более сложными соображениями, но при возможности получения товаров от внешне­го поставщика задачу можно свести к закрытой модели.

Четвертый тип ограничений (x_ij>0) означает, что товары пере­возятся от поставщиков потребителям, т. е. исключаются встреч­ные перевозки.