Реализация товаров по универмагу

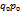
Ткань, м	Продано в базисном периоде по ценам базисного периода, у.е.	Индивидуальные индексы физического объема
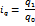
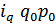
Шерсть	1520,0	1,2	1824,0
Сукно	2846,0	0,95	2703,7
Сатин	4795,0	1,02	4890,9
Итого	9161,0		9418,6

Пользуясь приведенными в таблице расчетами, подставим необходимые данные в формулу среднеарифметического индекса физического объема товарооборота

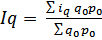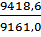= = 1,028, или 102,8%.

Таким образом, физический объем товарооборота в отчетном периоде по сравнению с базисным увеличился в среднем на 2,8%, а в абсолютном выражении продажа указанных товаров увеличилась на 9418,6 – 9161,0 = 257,6 у.е.

Следовательно, преобразование агрегатного индекса с базисными весами путем осреднения индивидуальных индексов приводит к среднеарифметическому индексу.

Покажем теперь преобразование агрегатного индекса в среднегармонический на примере индекса цен.

В тех случаях, когда неизвестны отдельные значения p₁ и q₁, а дано их произведение p₁ q₁ , т.е. товарооборот отчетного периода, и индивидуальные индексы цен i_р = 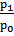, а сводный индекс должен быть исчислен с отчетными весами, применяется среднегармонический индекс цен. Причем индивидуальные индексы должны быть взвешены таким образом, чтобы среднегармонический индекс совпал с агрегатным. Из формулы i_р = 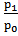определяем неизвестное значение р₀ и, заменив в агрегатной формуле индекса цен 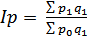значение р₀ = 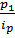, получим:

.

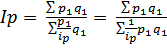Индекс в такой форме называется среднегармоническим индексом.

Например, определим средний размер снижения цен на продукты в текущем году.