Тангенсом острого угла прямоугольного теругольника называется отношение противолежащего катета к прилежащему

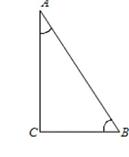
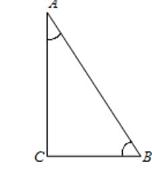
Например, для треугольника, который изображен на рисунке, ,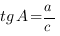

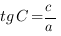
Задачи на нахождение сторон и углов прямоугольного треугольника решаются по такому алгоритму:

1. Выделяем треугольник, в который входит сторона или угол, который нам нужно найти.

2. Смотрим, какие элементы треугольника нам известны, и с помощью какой тригонометрической функции они между собой связаны.

3. Записываем соотношение, которое связывает между собой эти элементы,

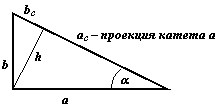
Теорема Пифагора: 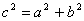Площадь: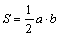

Тригонометрические соотношения: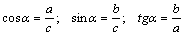

Центр описанной окружности лежит на середине гипотенузы.

Радиусы окружностей: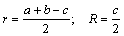

Высота, опущенная на гипотенузу: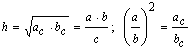

Катеты: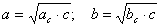

Примеры:

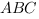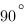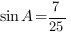1. В треугольникеуголравен,. Найдите.

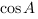Решение:

Так как требуется найти косинус угла, синус которого известен, мы можем воспользоваться основным тригонометрическим тождеством.

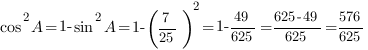
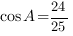
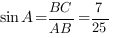
Ответ: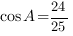

2. В треугольнике ABC угол C равен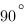,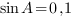. Найдите.

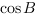Решение:

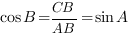
Значит,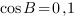

Ответ: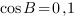

3. В треугольнике ABC угол C равен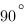,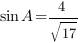. Найдите.

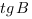Решение:

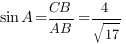
Введем единичный отрезок 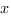, тогда ,

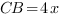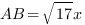
По теореме Пифагора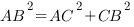

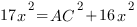
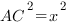
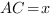
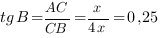
Ответ: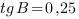

4. В треугольнике ABC угол C равен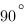,,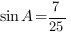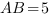. Найдите AC.

Решение:

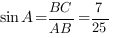
Введем единичный отрезок 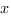, тогда ,

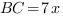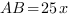
По теореме Пифагора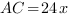

Найдем 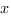: 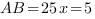– по условию.

Значит, 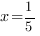. Отсюда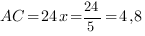

Ответ: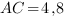

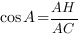, отсюда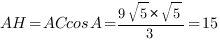

Ответ: AH=15.

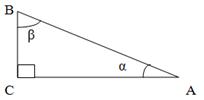
5.Задача.
В треугольнике АВС угол С равен 90 градусам. cos α = 4/5. Надите sin α, sin β

Решение.

Поскольку cos α = 4/5, то AC / AB = 4 / 5. То есть стороны соотносятся как 4:5. Обозначим длину AC как 4x, тогда AB = 5x.

По теореме Пифагора:
BC² + AC² = AB²

Тогда
BC² + (4х)² = (5х)²
BC² + 16х² = 25х²
BC² = 9х²
BC = 3x

sin α = BC / AB = 3x / 5x = 3/5
sin β = AC / AB, а его значение и так известно по условию, то есть 4/5

Ответ: 3/5, 4/5

Список литературы:

1. Апанасов П.Т. Сборник задач по математике: Учебное пособие для техникумов. -М.:Высш.шк., 1987. -Глава 1, §11, стр. 19.