Например, в результате проверки 1000 партий одинаковых изделий получено следующее распределение кол-ва бракованных изделий в партии

Оценка существенности показателей асимметрии и эксцесса позволяет сделать вывод о том, можно ли отнести данное эмпирическое распределение к типу кривых нормального распределения

Рис. 2. Ряды распределения с положительным (а) и отрицательным (б) эксцессом

В статистике распространены различные виды теоретических распределений: нормальное. биномиальное, Пуассона и др. Каждое из теоретических распределений имеет свою специфику и область применения.

Биномиальное распределение применяется при изучении распределений по альтернативным признакам, характеризующимся определенной вероятностью появления или отсутствия изучаемого события. Это распределение именуется так из-за его отношения к разложению двучлена (p+q)ⁿ. Вероятность того, что событие наступит равна p, вероятность того, что событие не наступит равна (1-р)=q. И, следовательно, p+q=1. Члены p и q относятся к вероятности наступления или ненаступления только одного события. Для двух событий вероятность наступления события по з-ну умножения равна р², вероятность наступления в первом случае и ненаступления во втором равна p*q, вероятность ненаступления в первом и наступления во втором равна q*p, ненаступления двух событий q². Общая вероятность может быть представлена алгебраически и равна р² + 2pq+ q² или (p+q)² . Для трех событий р³ + 3pq²+3p²q +q³. или (p+q)³

Распределение Пуассона используется при анализе распределения маловероятных и редко встречающихся событий. И имеет следующий вид:

,

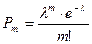где 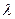-среднее число появления событий в одинаковых независимых испытаниях ( 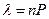-вероятность события при одном испытании), m- частота данного события.

Например, в результате проверки 1000 партий одинаковых изделий получено следующее распределение кол-ва бракованных изделий в партии.

Таблица 1

Количество брака	m1						Итого
Количество партий, содержащих данное число бракованных изделий	f1
Теоретическая частота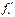

определим среднее число бракованных изделий в партии:

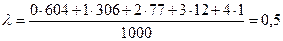
Находим теоретические частоты закона Пуассона:

,

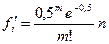m_i=0 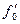=1000*0,606=606

m_i=1 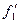=1000*0,5*0,606=303

m_i=2 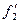=(1000*0,25*0,606)/2=76

m_i=3 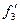=(1000*0,125*0,606)/6=13

m_i=4 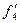=(1000*0,125*0,5*0,606)/24=2