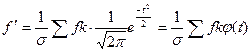2015-04-30
334
, где
Величина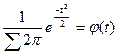 
есть функция от t, или плотность нормального распределения, которой определяется по специальной таблице.
Пример. Расчет теоретических частот и выравнивание эмпирического распределения по кривой нормального проиллюстрируем на данных о распределении филиалов почтовой связи по численности работников (х) (табл. 2).
Таблица 2
Выравнивание по кривой нормального распределения
| x | f |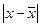 
| 
| 
| 
|
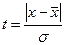
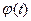
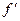
| 45,2 | 2,5 | 0,0175 | 1,2 | ||
| 35,2 | 1,9 | 0,0656 | 4,5 | ||
| 25,2 | 1,4 | 0,1497 | 10,2 | ||
| 15,2 | 0,8 | 0,2897 | 19,8 | ||
| 5,2 | 0,3 | 0,3814 | 26,0 | ||
| 4,8 | 0,3 | 0,3814 | 26,0 | ||
| 14,8 | 0,8 | 0,2897 | 19,8 | ||
| 24,8 | 1,4 | 0,1497 | 10,2 | ||
| 34,8 | 1,9 | 0,0656 | 4,5 | ||
| Итого | - | - | - | 122,2 |
Для расчетов были привлечены следующие данные, полученные на основе эмпирического ряда распределения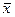 
= 235,2 чел, 
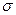= 18,3 чел., интервал к = 10 Последовательность расчетов определяют нормированные отклонения t для всех вариантов, по табл. Приложения 2 устанавливают соответствующие им значения функции 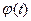умножение которых на величину
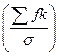= (125•10)/18,3 = 68,3 дает теоретические частоты .
|
|
|
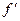Т.к. закон нормального распределения лежит в основе многих теорем статистики, применяемых для оценки представительности выборки, измерения связей, построения статистических критериев, то целесообразно рассмотреть правила проверки гипотезы о соответствии эмпирического распределения теоретическому закону нормального распределения.
