Логистическая регрессия – полезный классический инструмент для решения задачи регрессии и классификации. В последние годы логистическая регрессия получила распространение в скоринге для расчета рейтинга заемщиков и управления кредитными рисками. Поэтому, несмотря на свое «происхождение» из статистики, логистическую регрессию и ROC- анализ (аппарат для анализа качества моделей) почти всегда можно увидеть в наборе Data Mining алгоритмов.
Основная цель данного метода, как и множественного регрессионного анализа вообще, состоит в выявлении связи между несколькими независимыми переменными (называемыми также регрессорами или предикторами) и зависимой переменной. Бинарная логистическая регрессия применяется в тех случаях, когда зависимая переменная может принимать только два значения. Иными словами, с ее помощью можно оценить
вероятность того, что одна из двух альтернатив наступит для конкретного испытуемого (например, возврат кредита/дефолт).
Например, при множественной линейной регрессии предполагается, что зависимая переменная является линейной функцией независимых переменных, то есть:
у = а + bхх1 + b2х2 +... + bпхп.
Эту модель можно использовать для оценки вероятности исхода события. Если параметры хi характеризуют заемщика, то, определив стандартные коэффициенты регрессии bi и рассчитав величину у, можно интерпретировать ее как вероятность возврата долга.
Для расчета коэффициентов логистической регрессии можно применять любые градиентные методы: метод сопряженных градиентов, методы переменной метрики и другие.
ROC-кривая (Receiver Operator Characteristic) – кривая, которая наиболее часто используется для представления результатов бинарной классификации в машинном обучении.
Предположим, у нас имеется бинарная модель, предсказывающая, что заемщик с параметрами хi вернет долг с вероятностью Р. Как воспользоваться ею практически? Очевидно, нужно выдвинуть некий критерий в виде порогового уровня вероятности: например, при Р > 0,8 кредит предоставляется, а в противном случае (при Р ≤ 0,8) в кредите будет отказано. Значение Р = 0,8 будет выполнять роль так называемой точки (порога) отсечения (cut-off value), в соответствии с которым все множество потенциальных заемщиков делится на два класса: «хороших» и «плохих» клиентов банка. При этом предполагается, что имеется некоторый параметр, при изменении которого это разбиение будет меняться. Например, если вместо критерия Р = 0,8 мы примем Р = 0,6, многие клиенты, которые раньше считались «плохими», перейдут в класс «хороших».
В логистической регрессии порог отсечения изменяется от 0 до 1 – это и есть расчетное значение уравнения регрессии. Будем называть его рейтингом. Для оценки качества данной модели необходимо более детально рассмотреть ошибки, которые могут возникнуть при ее использовании.
Очевидно, при любой бинарной классификации их может быть только две:
– принять положительный случай за отрицательный (например, добросовестного заемщика за банкрота) – ошибка первого рода;
– отрицательный – за положительный – ошибка второго рода.
Для понимания сути ошибок I и II рода рассмотрим четырехпольную таблицу сопряженности (confusion matrix), которая строится на основе результатов классификации моделью и фактической (объективной) принадлежностью примеров к классам.
| Фактически | ||
| Модель | положительно | отрицательно |
| Положительно | TP | FP |
| Отрицательно | FN | TN |
TP (True Positives) – количество верно классифицированных моделью положительных примеров (так называемые истинно положительные случаи);
TN (True Negatives) – количество верно классифицированных от- рицательных примеров (истинно отрицательные случаи);
FN (False Negatives) – количество положительных примеров, классифицированных моделью как отрицательные (ошибки первого рода);
FP (False Positives) – количество отрицательных примеров, классифицированных как положительные (ошибки второго рода).
При оценке модели важную роль играют следующие соотношения, выраженные в процентах:
– доля истинно положительных примеров, распознанных моделью (True Positives Rate):
𝑇𝑇𝑃𝑃𝑇𝑇 = 𝑇𝑇𝑇𝑇
 𝑇𝑇𝑇𝑇+𝐹𝐹𝐹𝐹
𝑇𝑇𝑇𝑇+𝐹𝐹𝐹𝐹
∙ 100 %;
– доля ложно положительных примеров (False Positives Rate), то есть
отношение истинно отрицательных примеров, классифицированных данной моделью как положительные, к общему числу таких примеров:
𝐹𝐹𝑃𝑃𝑇𝑇 = 𝐹𝐹𝑇𝑇
 𝑇𝑇𝐹𝐹+𝐹𝐹𝑇𝑇
𝑇𝑇𝐹𝐹+𝐹𝐹𝑇𝑇
∙ 100 %.
Очевидно, что чем мягче критерий отбора «хороших» клиентов, тем
больше кредитоспособных заемщиков будут признаны таковыми и тем ближе величина TPR к 100 %. Но одновременно будет возрастать и доля ошибок второго рода, доля неверно квалифицированных «плохих» клиентов, отражаемая показателем FPR.
Введем еще два определения: чувствительность и специфичность модели. Ими определяется объективная ценность любого бинарного классификатора.
Величина Se = TPR называется также чувствительностью модели
(Sensitivity),
 𝐶𝐶𝐶𝐶 = TPR =
𝐶𝐶𝐶𝐶 = TPR =
TP TP + FN
· 100 %
а величина Sp = 100 – FPR, характеризующая долю верно распознанных
отрицательных случаев, – ее специфичностью (Specificity).
𝑇𝑇𝑇𝑇
 𝐶𝐶𝑆𝑆 =
𝐶𝐶𝑆𝑆 =
𝑇𝑇𝑇𝑇 + 𝐹𝐹𝑃𝑃
· 100 %
FPR =100 – Sp.
Эти два показателя определяют объективную ценность любого бинарного классификатора. Когда один из них стремится к нулю, другой принимает значения, близкие к 100, и наоборот (поскольку, как мы только что заметили, величины TPR и FPR всегда изменяются в одном направлении).
Сами термины чувствительность и специфичность, не очень понятные в контексте задачи кредитного скоринга, происходят из теории систем обработки сигналов; под чувствительностью здесь понимается способность воспринимающего устройства (Receiver) распознать полезный сигнал, под специфичностью – отсечь бесполезный сигнал (шум). Если провести аналогию с рассматриваемой нами задачей, «полезным сигналом» для банка будет запрос на кредит со стороны добросовестного заемщика, а «шумом» – со стороны банкрота.
Модель с высокой чувствительностью часто дает истинный результат при наличии положительного исхода (обнаруживает положительные примеры).
Наоборот, модель с высокой специфичностью чаще дает истинный результат при наличии отрицательного исхода (обнаруживает отрицательные примеры).
Для наглядного отображения указанных характеристик используется так называемая ROC-кривая (Receiver Operator Characteristic), которая строится следующим образом.
1. Для каждого значения порога отсечения, изменяемого с шагом dх (например, 0,01) от 0 до 1, рассчитывают значения чувствительности Se и специфичности Sp (в качестве альтернативы можно просто взять каждое последующее значение примера в выборке).
2. Строят график зависимости TPR от FPR:
– по оси ординат (Y) откладывают значение чувствительности Se = TPR (доля истинно положительных случаев),
– по оси абсцисс (X) – величину FPR = 100 – Sp (доля ложно положительных случаев).
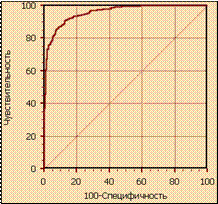
В результате вырисовывается ROC-кривая (рис. 6.1).
Полученный график обычно дополняют диагональной линией TPR = FPR.
Для идеального классификатора график ROC-кривой проходит через верхний левый угол, где доля истинно положительных случаев составляет 100 % или 1,0 (идеальная чувствительность), а доля ложно положительных примеров равна нулю. Поэтому чем ближе кривая к верхнему левому углу, тем выше предсказательная способность модели. Наоборот, чем меньше изгиб кривой и чем ближе она расположена к диагональной прямой, тем менее эффективна модель. Диагональная линия соответствует
«бесполезному» классификатору, т.е. полной неразличимости двух классов.
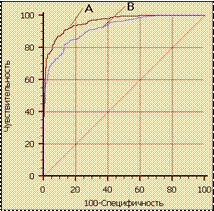
| Рисунок 6.1 – ROC-кривая | Рисунок 6.2 – Сравнение ROC-кривых |
При визуальной оценке ROC-кривых расположение их относительно друг друга указывает на их сравнительную эффективность. Кривая, расположенная выше и левее, свидетельствует о большей предсказательной
способности модели. Так, на рисунке (рис. 6.2) две ROC-кривые совмещены на одном графике. Видно, что модель «A» лучше.
Сравнение ROC-кривых
Иногда ROC-кривые располагаются достаточно плотно или пе- ресекаются, и их визуальное сравнение затруднено. В этом случае для оценки
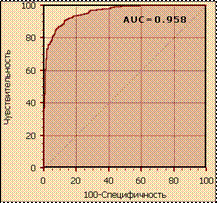 эффективности модели можно использовать площадь под кривой (AUC, Area Under Curve). Поскольку ROC-кривая всегда расположена выше диагонали, треугольник под диагональю площадью 0,5 всегда входит в состав измеряемой области. Таким образом, показатель AUC может изменяться от 0,5 («бесполезный» классификатор) до 1,0 (идеальная модель) (рис. 6.3).
эффективности модели можно использовать площадь под кривой (AUC, Area Under Curve). Поскольку ROC-кривая всегда расположена выше диагонали, треугольник под диагональю площадью 0,5 всегда входит в состав измеряемой области. Таким образом, показатель AUC может изменяться от 0,5 («бесполезный» классификатор) до 1,0 (идеальная модель) (рис. 6.3).
В литературе иногда
Рисунок 6.3 – Площадь под кривой
(показатель AUC)
которой можно судить о качестве модели:
приводится следующая экспертная шкала для значений AUC, по
| Интервал AUC | Качество модели |
| 0.9–1.0 | Отличное |
| 0.8–0.9 | Очень хорошее |
| 0.7–0.8 | Хорошее |
| 0.6–0.7 | Среднее |
| 0.5–0.6 | Неудовлетворительное |
Идеальная модель обладает 100 % чувствительностью и специфичностью. Однако на практике добиться этого невозможно, более того, невозможно одновременно повысить и чувствительность, и специфичность модели. Компромисс находится с помощью порога отсечения, т.к. пороговое значение влияет на соотношение Se и Sp. Можно говорить о задаче нахождения оптимального порога отсечения (optimal cut-off value).
В качестве критерия оптимальности могут, в частности, выступать следующие условия:
1) максимальная чувствительность при заданном уровне специ- фичности (например, при специфичности не ниже 80 %);
2) максимальная специфичность при заданном уровне чувстви- тельности (например, при чувствительности не ниже 80 %);
3) максимальная сумма чувствительности и специфичности модели
Se + Sp → max);
4) достижение баланса между чувствительностью и специфичностью (Se → Sp).
Если принимается последний вариант, оптимальный порог отсечения (точка баланса) соответствует точке пересечения двух кривых (чувствительности и специфичности).
Данный вариант представлен на рисунке (рис. 6.4).
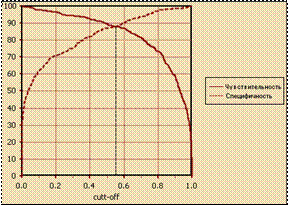
Рисунок 6.4 – Достижение баланса между чувствительностью и специфичностью
Порог – точка пересечения двух кривых, по оси X откладывается порог отсечения, а по оси Y –чувствительность или специфичность модели.
1) Импортируйте в новый проект (в файл L6_1.ded) данные из текстового файла loans_demo.txt, в котором хранится информация о заемщиках банка. При импорте исправьте типы полей, как указано на рисунке (рис. 6.5).
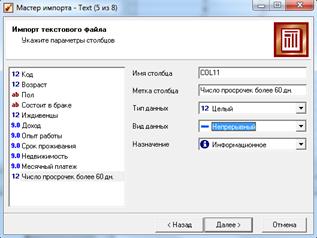
Рисунок 6.5 – Параметры типа полей
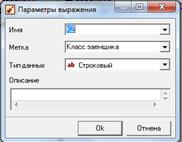
2) Необходимо уточнить, по каким правилам следует относить заемщиков к одному из двух классов («хороший» или «плохой»), используя данные о возврате ими долга (рис. 6.6).
Будем считать, что для физических лиц обслуживание долга признается плохим, если в течение последних 180 календарных дней имеются платежи по основному долгу и (или) по процентам, просроченным более чем на 60 календарных дней.
В данном случае в файле loans_demo.txt последний столбец, ха- рактеризующий качество обслуживания долга заемщиком, представлен полем Число просрочек свыше 60 дн. Остальные поля (кроме информационного поля Код ) содержат социально-экономические характеристики заемщиков: их возраст, пол, доход и др.
Из поля Число просрочек более 60 дн. получим новое поле Класс заемщика.
Для этого с помощью обработчика Калькулятор создадим строковое
поле и в строке функции напишем условный оператор (Если Число просрочек
>0, то Класс заемщика – плохой, иначе – хороший) (рис. 6.7).
Результат приведен на рис. 6.8.
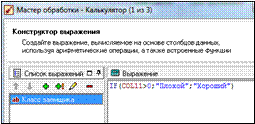
| Рисунок 6.6 – Параметры класса заемщика | Рисунок 6.7 – Запуск обработчика калькулятор |
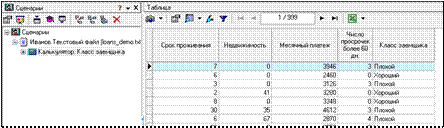
Рисунок 6.8 – Результат работы правил, к какому из двух классов относить заемщиков
3) Добавим в ветвь сценария обработчик Логистическая регрессия и на первом шаге Мастера зададим входные и выходные значения столбцов (рис. 6.9).
Поле Код будет информационным, Число просрочек более 60 дн. –
неиспользуемым, Класс заемщика – выходным, остальные поля – входными.
После щелчка по кнопке Настройка нормализации появится диалоговое окно (рис. 6.10).
Для логистической регрессии необходимо настроить:
– способы кодирования дискретных входных полей (битовая маска или уникальные значения);
– значения положительного и отрицательного событий для выходного поля.
В рассматриваемом случае имеется два входных дискретных поля – Пол и Состоит в браке. Для них рекомендуется указать способ кодирования Уникальные значения. Порядок списка таких значений влияет на кодирование значений полей. Так, для поля Пол первое уникальное значение («женский») будет закодировано нулем, второе («мужской») – единицей. Это значит, что при расчете кредитного рейтинга по уравнению логистической регрессии
женщинам всегда будет начисляться 0 баллов, а мужчинам – какой-либо отличный от нуля балл (рис. 6.11).
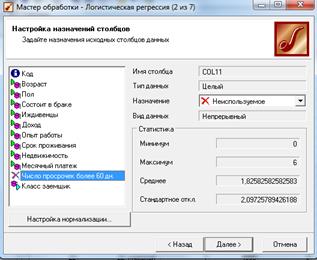
Рисунок 6.9 – Мастер обработки Логистическая регрессия
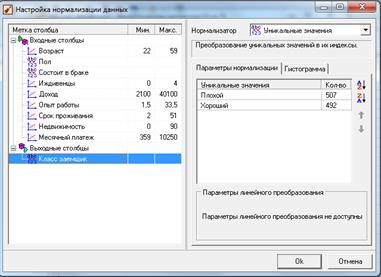
Рисунок 6.10 – Настройка нормализации данных

Рисунок 6.11 – Кодирование по уникальным значениям Пол
Аналогичным образом для поля Состоит в браке зададим кодирование по уникальным значениям в следующем порядке: «нет» (значение 0), «да» (значение 1) (рис. 6.12).

Рисунок 6.12 – кодирование по уникальным значениям Состоит в браке
Для выходного поля Класс заемщика порядок сортировки уникальных значений (их всегда два) определяет тип события: первое – отрицательное, второе – положительное. В данном случае, чем выше рейтинг – тем выше кредитоспособность, поэтому значение «хороший» будет положительным исходом события, а «плохой» – отрицательным (рис. 6.13).

Рисунок 6.13 – Преобразование уникальных значений
4) В следующих окнах Мастера будет предложено настроить обу- чающие и тестовые множества, а также изменить параметры алгоритма логистической регрессии. По умолчанию предлагается порог классификации, равный 0,5 (рис. 6.14), (рис. 6.15).
5) После щелчка по кнопке Пуск в последнем окне будет построена модель, и нужно будет выбрать визуализаторы узла (рис. 6.16). Отметим флажками следующие: ROC-анализ, Коэффициенты регрессии, Что-если, Таблица сопряженности, Таблица.
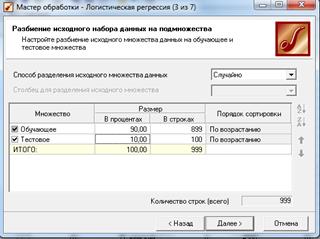
Рисунок 6.14 – Настройка обучающего и тестового множеств
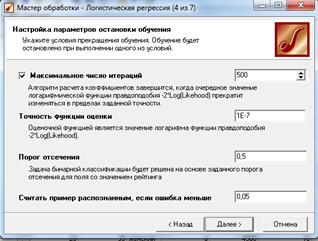
Рисунок 6.15 – Изменение параметров логистической регрессии
6) Визуализатор Таблица показывает, что после применения обра- ботчика Логистическая регрессия в массиве данных появились две новые колонки: Класс заемщика_OUT и Класс заемщика Рейтинг. Рейтинг представляет собой значение независимой переменной у, рассчитанное по уравнению логистической регрессии, а первое поле – принадлежность случая
к тому или иному классу в зависимости от установленного порога классификации (в данном случае он равен 0,5) (рис. 6.17).
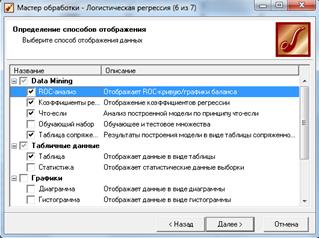
Рисунок 6.16 – Выбор способа отображения данных

Рисунок 6.17 – Логистическая регрессия отображена визуализатором Таблица
7) Визуализатор Коэффициенты регрессии дает информацию о влиянии факторов (входных параметров модели) на результат (рис. 6.18). Например, каждый дополнительный иждивенец уменьшает кредитный рейтинг заемщика на 1,87, а каждый дополнительный год стажа работы увеличивает его на 0,0031.
8) Визуализатор ROC-анализ выводит график ROC-кривой, на котором по умолчанию отмечается (желтым квадратным маркером) текущий порог отсечения, значения чувствительности и специфичности, показатель AUC и типы событий (рис. 6.19). В данном случае площадь под кривой AUC = 0,959 на обучающем множестве (кнопка  ) и AUC = 0,938 на тестовом
) и AUC = 0,938 на тестовом
 (кнопка), что говорит об очень хорошей предсказательной способности построенной модели.
(кнопка), что говорит об очень хорошей предсказательной способности построенной модели.
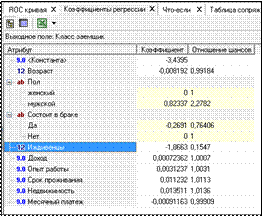
Рисунок 6.18 – Результат визуализации Коэффициентом регрессии
Оптимальный порог отсечения для данной модели не равен предварительно установленной величине 0,5; чтобы определить его, нужно в выпадающем меню кнопки  выбрать пункт Максимум (рис. 6.20).
выбрать пункт Максимум (рис. 6.20).
Оказывается, что максимум суммарной чувствительности и специфичности достигается в точке 0,45, для которой чувствительность Se = 90 %, специфичность Sp = 89 %. Это означает, что 90 % благонадежных заемщиков будут выявлены классификатором, а 100 – 89 = 11 % недобросовестных заемщиков получат одобрение при запросе кредита (кредитный риск).
Для установки нового порога отсечения, равного 0,45, необходимо перенастроить узел-обработчик логистической регрессии, нажав кнопку  . Результат можно посмотреть в визуализаторе Таблица (рис. 6.21).
. Результат можно посмотреть в визуализаторе Таблица (рис. 6.21).
9) Нетрудно видеть, что скоринговая модель с высокой специфичностью соответствует консервативной кредитной политике (чаще происходит отказ в выдаче кредита), а с высокой чувствительностью – политике рискованных кредитов. В первом случае минимизируется кредитный риск, вызванный неплатежами, во втором – коммерческий риск, связанный с упущенной выгодой.
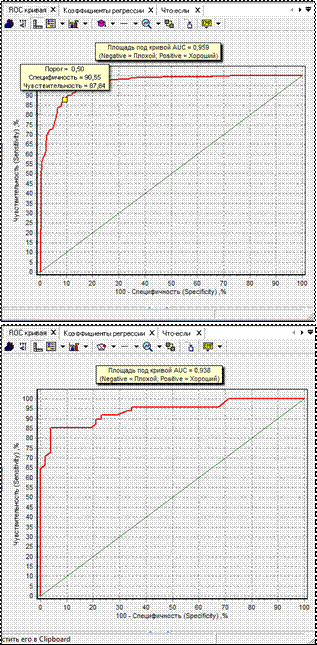
Рисунок 6.19 – Результат визуализации ROC-анализ
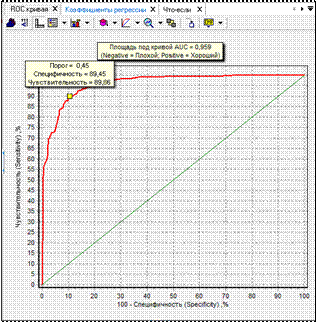
Рисунок 6.20 – Результат визуализации ROC-анализ с оптимальным порогом отсечения
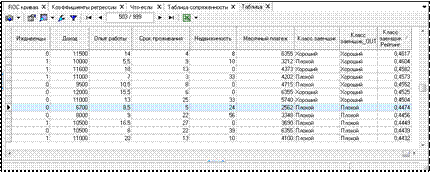
Рисунок 6.21 – Результат визуализации Таблица
Это хорошо иллюстрирует визуализатор Таблица сопряженности (рис. 6.22). Он позволяет сравнить категориальные значения выходного поля исходной выборки (обучающей или тестовой) с рассчитанными по модели с выбранным порогом отсечения (в данном случае – 0,45).
На обучающем множестве (рабочая выборка) модель реже отказывала в выдаче «хорошим» заемщикам (45 ошибочных случаев) и чаще выдавала кредит «плохим» клиентам (48); точность классификации составила 89 % (407 + 399): 899 = 89 %). На тестовом множестве наблюдается примерно та же картина (точность классификации (40 + 43): 100 = 83 %). Если такое решение не соответствует кредитной политике банка, можно поднять порог отсечения и добиться того, чтобы модель чаще выдавала отрицательное решение.


| а | б |
| Рисунок 6.22 – Результат визуализации Таблица сопряженности |
10) Визуализатор Что-если позволяет определить, как будет вести себя построенная модель при подаче на ее вход тех или иных данных. Другими словами, проводится эксперимент, в котором, изменяя значения входных полей обучающей или рабочей выборки для модели логистической регрессии, можно увидеть, как изменяются выходные значения модели (рис. 6.23).
Окно визуализатора включает два представления – табличное и графическое, которые формируются одновременно. В верхней части таблицы отображаются входные поля, в нижней -выходные и расчетные. Изменяя значения входных полей, пользователь дает команду на выполнение расчета и может отслеживать значения, получаемые на выходе логистической регрессии.
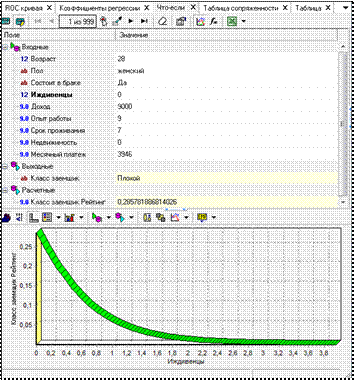
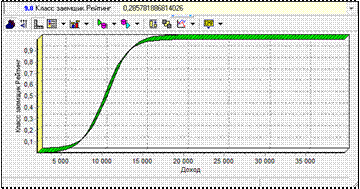
Рисунок 6.23 – Отслеживание значений, получаемых на выходе логистической регрессии.
Сохраните результаты в файл L6_1.ded.
 2015-04-30
2015-04-30 9238
9238








