Дадим основные понятия и определения, проиллюстрировав их на основе рисунка 4.1

Чередующаяся последовательность v₀(v₀,v₁)v₁(v₁,v₂)v₂…(v_l-1,v_l)v_l вершин и ребер графа называется маршрутом, соединяющим вершины v₀ и v_l.

Маршрут называется цепью, если все его ребра различны:

1 (1, 2) 2 (2, 3) 3 (3, 4) 4 (4, 2) 2 (2, 5) 5.

Цепь называется простой, если все ее вершины различны:

1 (1, 4) 4 (4, 5) 5.

Цепь, у которой v₀ совпадает с v_l и все ребра различны, называется циклом:

1 (1, 2) 2 (2, 3) 3 (3, 4) 4 (4, 2) 2 (2, 5) 5 (5, 1) 1.

Цикл является простым, если все его вершины различны кроме начальной v₀ и конечной v_l, которые совпадают:

1 (1, 4) 4 (4, 2) 2 (2, 5) 5 (5, 1) 1.

Граф (сеть) называется связным, если любые две его несовпадающие вершины соединены маршрутом (граф на рис. 4.1 - связный). В противном случае – несвязным (см. рис. 4.2):

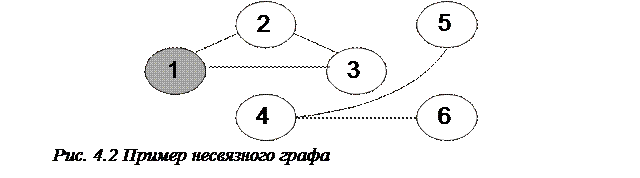
Граф называется взвешенным, если каждому его ребру поставлено в соответствие некоторое число w(l), называемое весом ребра.

Тогда под весом графа понимают суму весов всех его ребер, т.е. .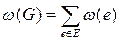

Связанный граф, не содержащий циклов, называется деревом:

Граф H =(V^/,E^/) называется остовным подграфом графа G=(V,E), если множество его вершин V^/ совпадает с множеством вершин графа G, а множество его ребер E^/ является подмножеством множества ребер G, т.е. V^/ = V, E^/ Í E.

Если остовный подграф H графа G является деревом, то H называется остовным деревом графа G (см. рис. 4.3):

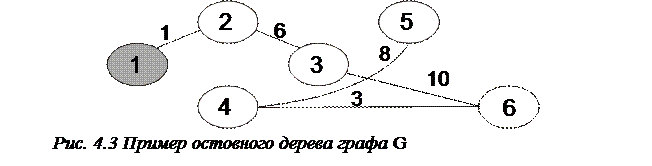
Ориентированный граф - это пара множеств (V,A), где V - множество вершин, A - множество ориентированных ребер, которые называются дугами. Если a=(v1, v2) - дуга, то вершины v₁ и v₂ называются ее началом и концом соответственно (см. рис. 4.4).

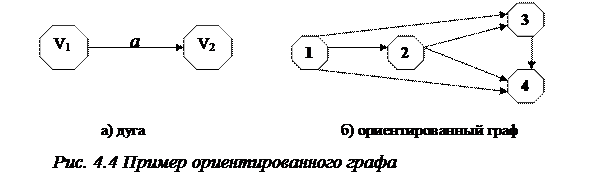
Если каждой дуге ориентированного графа поставлено в соответствие некоторое неотрицательное число w(l), т.е. w(l) ³ 0, " l Î A, называемое весом дуги, то ориентированный граф называется взвешенным.

4.3.2. Задача минимизации сети

Задача минимизации сети состоит в нахождении ребер, соединяющих все узлы сети (т.е. каждая пара узлов соединена цепью) и имеющих минимальную суммарную длину (или вес).

Очевидно, что решение задачи не должно содержать циклов. Отсутствие циклов в минимальной сети естественным образом приводит к понятию – минимальное остовное дерево, т.е. остовное дерево с минимальным весом.

Данная задача может быть сформулирована следующим образом:

В связном взвешенном графе (G, w) порядка n найти остовное дерево минимального веса, где w = w(e) – вектор весов ребер графа G, n–число вершин графа G.

Для ее решения имеются эффективные алгоритмы, применяемые к произвольному связному графу, необязательно полному.

Алгоритм Краскала

1. Строим граф T₁= O_n+l₁, присоединяя к пустому графу O_n на множестве вершин V графа G ребро минимального веса. Если таких ребер несколько, т.е. w(l₁)=w(l₂)=minw(l), то берется любое из этих ребер. Этот выбор ребра указывает на неоднозначность минимального остовного дерева.

2. Если граф T_i уже построен и i<n-1, то строим граф T_i+1=T_i+ l_i+1, где l _i+1 - ребро графа G, имеющее минимальный вес среди ребер, не входящих в T_i и не составляющих циклов с ребрами из T_{i .}

3. В противном случае, если i=n-1, алгоритм заканчивает свою работу, т.е. остовное дерево минимального веса построено. Граф T_i – искомое остовное дерево минимального веса.

Данный алгоритм на каждом шаге строит ациклический граф, необязательно связный на каждом шаге, кроме последнего.

Рассмотрим еще один алгоритм решения задачи о минимальном остовном дереве графа.

Алгоритм Прима

1. Выбираем ребро l₁=аb минимального веса и строим дерево T₁, полагая V₁={a,b}, E₁={l₁}.

2. Если дерево T_i порядка i+1 уже построено и i<n-1, то среди ребер, соединяющих вершины этого дерева с вершинами графа G, не входящими в T_i, выбираем ребро l _i+1 вместе с его не входящим в T_i концом.

3. Если i=n-1, алгоритм оканчивает работу, т.е. построено остовное дерево минимального веса. Граф T_i – искомое остовное дерево минимального веса.

Данный алгоритм на каждом шаге строит связный ациклический граф.

Примечание

В некоторых ситуациях требуется построить остовное дерево не минимального, а максимального веса. К этой задаче также применимы алгоритмы Краскала и Прима. Следует только всюду заменить минимальный вес на максимальный.

Пример 4.2

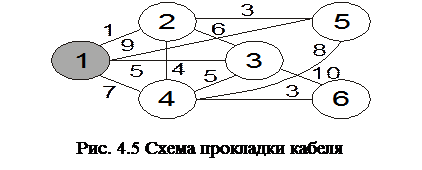
Телевизионная фирма планирует создание кабельной сети для обслуживания пяти районов-новостроек (см. рис. 4.5). Числа на ребрах указывают длину кабеля, соединяющего соответствующие узлы (вершины). Узел 1 представляет телевизионный центр, а остальные узлы (2-6) соответствуют пяти новостройкам. Отсутствие ребра между двумя узлами означает, что соединение соответствующих новостроек либо связано со слишком большими затратами, либо физически невозможно.

Нужно найти такие ребра, которые потребуют кабель минимальной длины для связи (прямой или через другие пункты) всех районов с телевизионным центром.

Решение:

1) Алгоритм Краскала:

а) упорядочим ребра графа в порядке убывания их весов:

w(l)	Е
	+	(1,2)
	+	(4,6)
	+	(2,5)
	+	(2,4)
	+ (-)	(1,3)
	- (+)	(3,4)
	-	(2,3)
	-	(1,4)
	-	(4,5)
	-	(1,5)
	-	(3,6)

//знаком «+» отмечены те рёбра, которые включаются в остовное дерево; в данное остовное дерево можно включить либо ребро (1, 3), либо ребро (3, 4)//

б) минимальная длина кабеля, соединяющего телестанцию с районами-новостройками, равна w=1+3+3+4+5=16 (км).

2) Алгоритм Прима:

В данном примере логично начинать с вершины "1", соответствующей телецентру.

T₁: V₁={1,2}, E₁={(1,2)};

T₂= T₁È(2,5): V₂ ={1,2,5}, E₂={(1,2), (2,5)};

T₃= T₂È(2,4): V₃ ={1,2,4,5}, E₃={(1,2), (2,5), (2,4)};

T₄= T₃È(4,6): V₄ ={1,2,4,5,6}, E₂={(1,2), (2,5), (2,4), (4,6)};

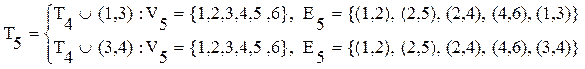
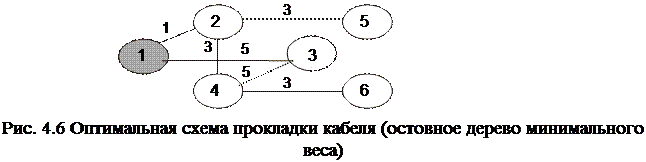
Так как i=n-1 =6-1=5, то остовное дерево минимального веса построено (см. рис. 4.6), т.е. Т₅:

w_min = 16 (км).

Ответ:

Оптимальная схема подключения районов новостроек к телевизионному центру показана на рис. 4.6. Ее практическая реализация потребует кабель минимальной длины – 16 км.

4.3.3. Задача о кратчайшем пути

Задача о кратчайшем пути формулируется обычно на ориентированных графах.

Пусть G=(V,A) - ориентированный взвешенный граф. Задача о кратчайшем пути состоит в отыскании пути минимального веса, соединяющего заданные начальную и конечную вершины графа G при условии, что хотя бы один путь существует.

Начальную и конечную вершины обозначим соответственно через s и t; (s,t) -путь минимального веса будем называть кратчайшим (s,t)-путем.

Рассмотрим случай, когда веса всех дуг графа неотрицательны, т.е. (w(l) ³0, " lÎA). Существует эффективный алгоритм построения кратчайшего пути в графе с неотрицательными весами дуг, предложенный Е. Дийкстрой в 1959 году.

Суть алгоритма. На каждой итерации этого алгоритма всякая вершина v графа G имеет метку l(v), которая может быть постоянной или временной. В первом случае l(v) -вес кратчайшего (s,v) -пути. Если же метка l(v) временная, то l (v) - вес кратчайшего (s,v) -пути, проходящего только через вершины с постоянными метками. Таким образом, временная метка l(v) является оценкой сверху для веса кратчайшего (s,v) -пути, и, став на некоторой итерации постоянной, она остается такой до конца работы алгоритма. Кроме l(v) с каждой вершиной v графа G, за исключением s, связывается еще одна метка - q(v). На каждой итерации q(v) являются номером вершины, предшествующей v в (s,v)- пути, имеющем минимальный вес среди всех (s,v)- путей, проходящих через вершины, получившие к данному моменту постоянные метки. После того, как вершина t получила постоянную метку, с помощью меток q(v) легко указать последовательность вершин, составляющих кратчайший (s,v) -путь.

Перед началом первой итерации алгоритма вершина S имеет постоянную метку l(s)=0, а метки l всех остальных вершин равны бесконечности и эти метки временные. Общая итерация алгоритма состоит в следующем. Пусть p - вершина, получившая постоянную метку l(p) на предыдущей итерации. Просматриваем все вершины VÎГ(р), имеющие временные метки, с целью уменьшения (если это возможно) этих меток; здесь Г(р) - множество всех вершин, имеющих временные метки и смежных с вершиной р. Метки l(v) вершины vÎГ(р) заменяются на l(p)+w(р,v), если оказалось, что l(v)>l(p)+w(р,v). В этом случае говорим, что вершина v получила свою метку l из вершины p, и полагаем q(v)=p.

Если же l(v) £ l(p) + w(р,v), то метки q и l вершины v не изменяются на данной итерации. Алгоритм заканчивает работу, когда метка l(t) становится постоянной. Тогда l(t) -вес кратчайшего (s,t)- пути, который обозначается Р^*. Этот путь определяется с помощью меток q так: P^* = (s,…, q³(t), q²(t), q(t), t).

Алгоритм Дийкстры:

1. Положить l(s) =0 и считать эту метку постоянной. Положить l(v) =¥, " v ÎV, v ¹ s, и считать эти метки временными. Положить p = s.

2. " vÎГ(р) с временными метками выполнить:

а) если l(v) >l(p) + w(р,v), то l(p) = l(p) + w(р,v); q(v) = p;

б) иначе l(v) и q(v) не менять.

3. Пусть V^/ - множество вершин с временными метками l. Найти вершину v^*, такую, что l(v^*)=min(v), vєV ^/. Считать метку l(v^*) постоянной меткой вершины v^*.

4. р = v^*. Если p=t, то перейти к пункту 5. Иначе перейти к пункту 2.

5. P^* = (s,…, q³(t), q²(t), q(t), t) - кратчайший путь. Конец.

Замечание:

1. Алгоритм Дийкстры применим к смешанным и, в частности, к неориентированным графам. Для этого достаточно каждое неориентированное ребро uv графа, имеющее вес w(u,v), рассмотреть как пару дуг (u,v) и (v,u) того же веса.

2. Если пункт 4 модифицировать так, чтобы алгоритм заканчивал работу только после получения всеми вершинами постоянных меток, то он будет строить кратчайшие пути из вершины s в каждую из остальных вершин.

Пример 4.3 Задача о замене оборудования

Содержательная постановка задачи

Фирма по прокату автомобилей планирует замену автомобильного парка на очередные пять лет. Автомобиль должен проработать не менее одного года, прежде чем фирма поставит вопрос о его замене. В таблице приведены стоимости замены автомобилей (в тыс.$), зависящие от времени замены и числа лет, в течении которых автомобиль находился в эксплуатации.

Построение математической модели

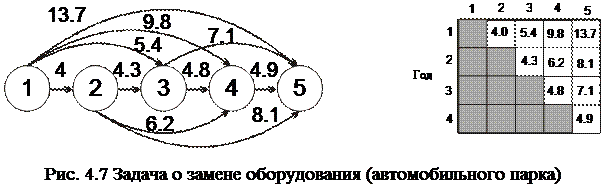
Эту задачу можно представить на сети в следующем виде (см. рис. 4.7). Каждому году ставится в соответствие определенный узел. Длина дуги, соединяющей два узла, равна соответствующей стоимости замены из таблицы. Задача сводится к нахождению кратчайшего пути между узлами 1 и 5.

Решение:

Решаем данную задачи с помощью построенной модели алгоритмом Дийкстры:

1) ;

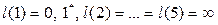2) ;

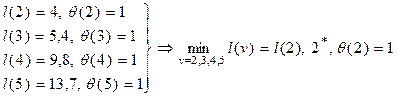3) ;

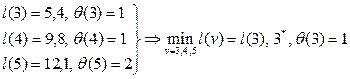4) ;

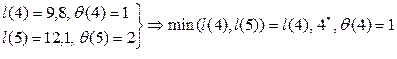5) .

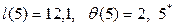Р^*= (1, 2, 5) – кратчайший путь из вершины 1 в вершину 5. Его длина будет минимальной и составит 9,8.

Ответ:

Таким образом, оптимальное решение 1®2®5 со стоимостью 12,1тыс.$. Это означает, что каждый автомобиль заменяется через два года, а через пять лет - списывается.

4.3.4Задача о максимальном потоке

Пусть G=(V, A) - ориентированный граф (сеть).

S^/єV называется истоком, если не существует дуг, оканчивающихся в S^/.

S^//єV называется стоком, если не существует дуг, начинающихся в S^//.

Пусть в G существует ровно один исток S^/ и один сток S^//.

Функция j: А®R₊ - пропускная способность, т.е. j (l) - пропускная способность дуги l, которая определяет максимальное количество потока проходящего по дуге l.

Потоком в графе называется функция m: А®R₊, обладающая свойствами:

1) " l 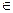A: 0£m(l)£j(l), где m (l) - поток через дугу l;

2) " u 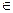V: u¹s ^/ и u¹s^//: .

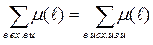Величиной потока называется число .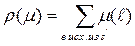

Теорема 4.4

В графе G = (V, A) суммарный поток по всем дугам, вышедшим из истока, равен суммарному потоку по всем дугам вошедшим в сток, т.е.:

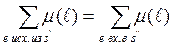(4.9)

Постановка задачи о максимальном потоке:

Пусть G = (V, A) имеет один исток и один сток. j: А® R₊ - пропускная способность дуг этого графа. М={m} - множество всех потоков через граф G, 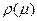- величина потока.

Среди всех потоков через граф G найти поток максимальной величины, т.е.:

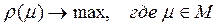. (4.10)