Пример 3: При изучениивлияния рекламы наразмер среднемесячного вклада было обследовано 2 банка. Получены следующие результаты.
Таблица 1. Зависимость вклада от рекламы.
| Размер месячного вклада, р. | Число вкладчиков | |
| Банк с рекламой | Банк без рекламы | |
| До 500 | - | |
| 500-520 | - | |
| 520-540 | - | |
| 540-560 | ||
| 560-580 | ||
| 580-600 | ||
| 600-620 | - | |
| 620-640 | - | |
| Итого: |
Определите:
1) Для каждого банка:
А) средний размер вклада за месяц; 
Б) дисперсию вклада;
2) средний размер вклада за месяц для двух банков;
3) дисперсию вклада для двух банков, зависящую от рекламы, 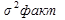 ;
;
4) дисперсию вклада для двух банков, зависящую от всех факторов, кроме рекламы 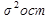 ;
;
5) общую дисперсию 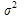 , используя правило сложения;
, используя правило сложения;
6) коэффициент детерминации 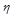 2;
2;
7) корреляционное отношение 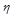 .
.
Решение: Рассчитаем групповые показатели для каждого банка. Показатели банка, использующего рекламу:
Расчет среднего вклада и дисперсии
| Размер месячного вклада, р. | Число вкладчиков f | Середина интервала x | x-a | x-a k | 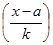 × f × f
| 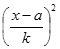
| 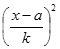 × f × f
|
| 540-560 | -40 | -2 | -22 | ||||
| 560-580 | -20 | -1 | -13 | ||||
| 580-600 | |||||||
| 600-620 | |||||||
| 620-640 | |||||||
| Итого: | - | - | - | -25 | - |
Представлен интервальный ряд распределения. Выражаем его дискретно, т.е. определяем середину интервала (гр.3).
Средний размер вклада 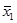 определим способом моментов:
определим способом моментов:
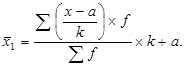
Обозначаем a и k. За a выбираем размер варианта при наибольшей частоте, т.е. a = 590, за k – размер интервала, т.е. k =20. Далее решение оформляем в таблицу, т.е. заполняем гр. 4, 5,6. Результаты вносим в формулу
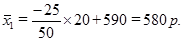
Средний вклад за месяц в банке с рекламой составляет 580р.
Определяем дисперсию вклада 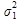 :
:
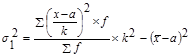
Для решения заполняем гр.7 и 8:
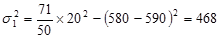
Такие же расчеты произведем для банка, не использующего рекламу:
| Размер месячного вклада, р. | Число вкладчиков f | Середина интервала, р. x | x-a | x-a k | 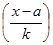 × f × f
| 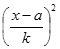
| 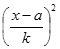 × f × f
|
| До 500 | -40 | -2 | -6 | ||||
| 500-520 | -20 | -1 | -4 | ||||
| 520-540 | |||||||
| 540-560 | |||||||
| 560-580 | |||||||
| 580-600 | |||||||
| Итого: | - | - | - | - |
Решение: Определяем середину интервала (гр.3).
Обозначаем a и k: a=530 (вариант при наибольшей частоте); k=20 (размер интервала). Определяем средний вклад за месяц 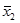 .
.
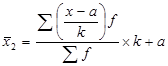
Заполняем гр. 4,5,6.
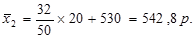
Средний вклад в банк без рекламы составил 542,8р.
Определяем дисперсию вклада 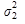 :
:
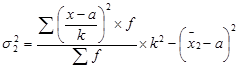
Заполняем гр. 7 и 8. Подставляя значения в формулу:
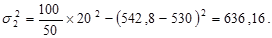
Далее определим средний вклад 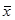 за месяц для двух банков. Так как в банках по 50 вкладчиков (частоты одинаковы), для расчета используем среднюю арифметическую простую:
за месяц для двух банков. Так как в банках по 50 вкладчиков (частоты одинаковы), для расчета используем среднюю арифметическую простую:
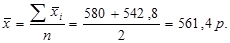
Средний вклад для двух банков составил 561,4 р. в месяц.
Определяем межгрупповую (факторную) дисперсию:
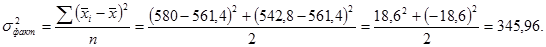
Определяем внутригрупповую (остаточную) дисперсию:
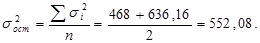
Теперь рассчитаем общую дисперсию 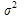 :
:
Используя правило сложения дисперсий
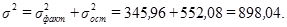
Рассчитаем коэффициент детерминации 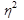 :
:
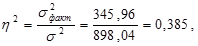
или 38,5%.
Далее определим корреляционное отношение 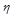 :
:
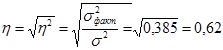
Ответ: Результаты показывают, что средний вклад в банке с рекламой выше, чем в банке без рекламы и в двух банках вместе. Следовательно, реклама положительно влияет на вклады. Коэффициент детерминации 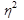 свидетельствует о том, что средний вклад на 38,5% зависит от рекламы. Корреляционное отношение
свидетельствует о том, что средний вклад на 38,5% зависит от рекламы. Корреляционное отношение 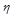 , равное 0,62, свидетельствует о достаточно тесной связи между рекламой и вкладом. Эмпирическое корреляционное отношение (индекс корреляции) может находиться в пределах от 0 до 1, чем он ближе к единице, тем теснее связь.
, равное 0,62, свидетельствует о достаточно тесной связи между рекламой и вкладом. Эмпирическое корреляционное отношение (индекс корреляции) может находиться в пределах от 0 до 1, чем он ближе к единице, тем теснее связь.
Подготовка к 1 контрольной работе (аналогичные задачи: задание 1,2 – стр. 22 Теории статистики, задание 3 – стр. 31 Теории статистики).
Задача 3. Для оценки стоимости основных средств промышленных предприятий региона проведен 5% механический отбор, результаты которого представлены в таблице:
Если 100 предприятий – 5%, то
X предприятий -100%
Решаем пропорцию
X = 100*100/ 5 = 2000 предприятий.
| Группы предприятий по стоимости основных средств, млрд.руб. | Число предприятий |
| До 1 | |
| 1-2 | |
| 2-3 | |
| 3-4 | |
| 4-5 | |
| 5 и выше | |
| Итого: |
Определить:
1) по выборочным предприятиям: а) среднюю стоимость основных средств; б) моду и медиану;
2) показатели вариации: а) размах вариации; б) среднее линейное отклонение; в) дисперсию и среднее квадратическое отклонение; г) коэффициент вариации;
3) с вероятностью 0,954 для всех промышленных предприятий региона: а) среднюю стоимость основных фондов; б) долю предприятий со стоимостью основных фондов выше 5 млрд. р.; в) ожидаемую сумму налога на имущество (2%) по региону в целом. Сделать выводы.
Решение:
| Группы предприятий по стоимости основных средств, млрд.руб. | Число предприятий f | x (середина интервала) | x-a | x-a k | 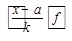
| 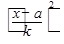
| 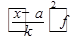
| 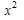
| 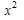 f f
| 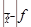
|
| До 1 | 0,5 | -2 | -2 | -24 | 0,25 | 26,64 | ||||
| 1-2 | 1,5 | -1 | -1 | -22 | 2,25 | 49,5 | 26,84 | |||
| 2-3 | 2,5 | 6,25 | 187,5 | 6,6 | ||||||
| 3-4 | 3,5 | 12,25 | 171,5 | 10,92 | ||||||
| 4-5 | 4,5 | 20,25 | 21,36 | |||||||
| 5 и выше | 5,5 | 30,25 | 302,5 | 27,8 | ||||||
| Итого: | - | - | - | - | 120,16 |
1) а) Определим k = 1, вариант x при наибольшей частоте f =30, a=2,5
Среднюю стоимость основных фондов рассчитаем методом моментов:
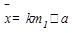 момент первого порядка:
момент первого порядка: 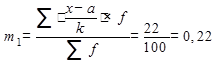
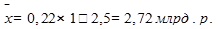
Б) мода
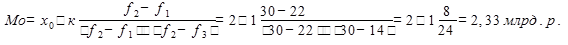
Медиана
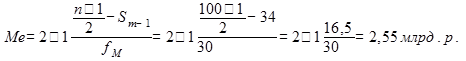
2) Показатели вариации:
А) размах вариации:  R=х мах – х мин =5,5-0,5=5 млрд.р.
R=х мах – х мин =5,5-0,5=5 млрд.р.
Б) среднее линейное отклонение:

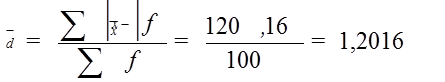
В) в) дисперсию по способу моментов и среднее квадратическое отклонение:
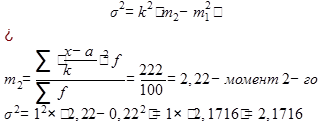
г) коэффициент вариации
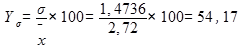
| P-вероятности | t – критерии доверия |
| 0.683 | 1.0 |
| 0.866 | 1.5 |
| 0.954 | 2.0 |
| 0.988 | 2.5 |
| 0.997 | 3.0 |
| 0.999 | 3.5 |
3) Дано: Р=0,954, критерий t=2
Определить среднюю стоимость основных фондов: поскольку мы уже определили выборочную среднюю (5% отбор – 100 предприятий, следовательно 100% - 2000 предприятий) 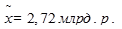 , то при заданной вероятности генеральная средняя будет находиться в следующих границах:
, то при заданной вероятности генеральная средняя будет находиться в следующих границах: 
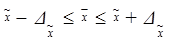
Найдем ошибку выборки: при известной дисперсии выборочной совокупности механическом повторном отборе для средней
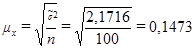 , следовательно
, следовательно 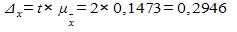 , значит
, значит 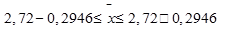 , откуда
, откуда 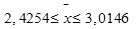 млрд.р. (пределы, в которых будет находиться генеральная средняя стоимость основных фондов).
млрд.р. (пределы, в которых будет находиться генеральная средняя стоимость основных фондов).
б) долю предприятий со стоимостью основных фондов выше 5 млрд. р.;
долю предприятий выбираем из таблицы, построенной нами, где видно, что доля этих предприятий составляет 10 или 10% от 100 выбранных.
Доверительные интервалы для генеральной доли:
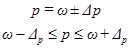
Найдем предельную ошибку для доли 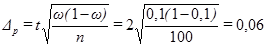
Находим доверительные интервалы для генеральной доли
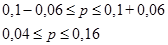 или доля предприятий со стоимостью основных фондов выше 5 млрд. р. будет колебаться от 4 до 16%.
или доля предприятий со стоимостью основных фондов выше 5 млрд. р. будет колебаться от 4 до 16%.
в) ожидаемую сумму налога на имущество (2%) по региону в целом.
Средняя стоимость основных фондов 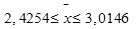 , количество предприятий по региону в целом 2000, следовательно
, количество предприятий по региону в целом 2000, следовательно 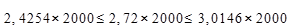 ,
,
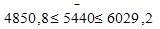
Начислим на средние суммы налога на имущество
Сделать выводы.
 2015-04-30
2015-04-30 1050
1050
