Дифференциальные уравнения движения материальной точки. Две основные задачи динамики точки

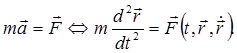
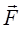− равнодействующая,

Декартова система координат:

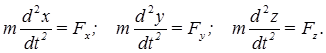
Естественная система координат:

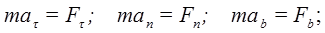
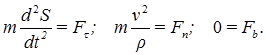
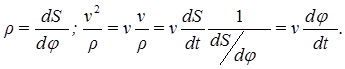Второе уравнение можно преобразовать:

Получаем для естественной системы координат:

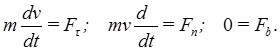
Первая (прямая) задача динамики точки: зная массу точки и ее закон движения, можно найти действующую на точку силу.

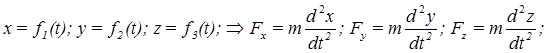
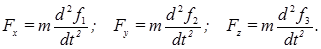
Зная проекции силы на координатные оси, легко определить мо­дуль силы и косинусы углов силы с осями координат.

Пример. Закон движения точки x = aCoskt; y = bSinkt, массы точки m. Определить траекторию и силу, под действием которой происхо­дит движение.

Уравнение траектории:

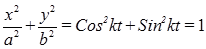
− эллипс с полуосями a, b

F_x= − mk²aCoskt; F_y= − mk²bSinkt или F_x= − mk²x; F_y= − mk²y;

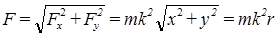
(r − радиус−вектор точки).

Косинусы углов силы F с осями координат:

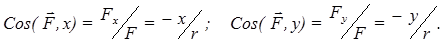
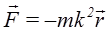Отсюда можно заключить, что сила F имеет направление, проти­воположное вектору r.

Окончательно.