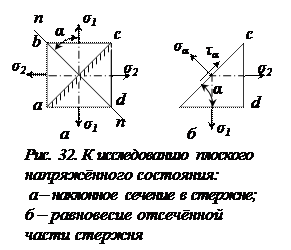
 Рассмотрим общий случай плоского (двухосного) напряжённого состояния, когда отличны от нуля два главных напряжения
Рассмотрим общий случай плоского (двухосного) напряжённого состояния, когда отличны от нуля два главных напряжения 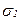 и
и 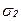 (рис. 32а). Между направлением напряжения
(рис. 32а). Между направлением напряжения 
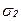 и площадкой угол равен
и площадкой угол равен 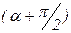 Из условия равновесия отсечённой правой части (рис. 32б) определим напряжения
Из условия равновесия отсечённой правой части (рис. 32б) определим напряжения 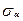 и
и 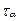 . Для этого воспользуемся уравнениями (6.1) и (6.2). Суммируя напряжения от действия
. Для этого воспользуемся уравнениями (6.1) и (6.2). Суммируя напряжения от действия 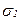 с напряжением от действия
с напряжением от действия 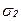 (заменяя угол α на угол (
(заменяя угол α на угол (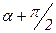 )), получим:
)), получим:
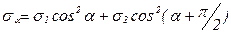 ,
,
откуда
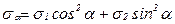 . (6.8)
. (6.8)
Аналогично
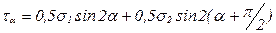
откуда 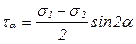 . (6.9)
. (6.9)
Из формулы (6.9) видно, что максимальное касательное напряжение равно полуразности главных напряжений (при 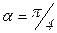 ):
):
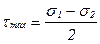 . (6.10)
. (6.10)
Из формул (6.8) и (6.9) следует:
1. Если 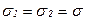 , то на всех площадках, проходящих через рассматриваемую точку, нормальное напряжение равно
, то на всех площадках, проходящих через рассматриваемую точку, нормальное напряжение равно 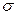 , а касательное напряжение равно нулю. Такое напряжённое состояние называют равномерным двухосным растяжением (или сжатием).
, а касательное напряжение равно нулю. Такое напряжённое состояние называют равномерным двухосным растяжением (или сжатием).
2. Если 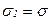 ,
, 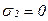 , а
, а 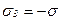 , то при
, то при 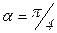 нормальное напряжение в наклонной площадке оказывается равным нулю, а
нормальное напряжение в наклонной площадке оказывается равным нулю, а 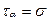 . Такое напряжённое состояние называется чистым сдвигом.
. Такое напряжённое состояние называется чистым сдвигом.
 2015-04-30
2015-04-30 430
430








