2015-04-30
4815
При проверке гипотез о значении параметра биномиального распределения рассматривают задачи следующих видов:
- сравнение вероятности «успеха» p в одном испытании с заданным p0;
- сравнение вероятностей «успеха» в двух сериях испытаний;
- сравнение вероятностей «успеха» в нескольких сериях испытаний.
Нулевые гипотезы для этих видов задач имеют соответствующий вид
,
,
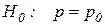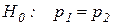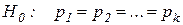
1. Задачи первого типа (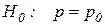) возникают, когда при достаточно большом числе n независимых испытаний, имеются основания предполагать, что неизвестная вероятность равна гипотетическому значению.
Пусть в n испытаниях по схеме Бернулли успех произошел m раз. В качестве статистики критерия выбирают относительную частоту p*=m/n. При больших значениях n (n>50) и при выполнении условий mp*>5, n(1-p*)>5 распределение случайной величины p* с достаточной для практических расчетов точностью аппроксимируется нормальным распределением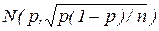 
. Отсюда следует, что если гипотеза 
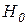верна, то статистика
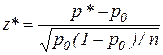
имеет распределение, близкое к нормальному распределению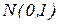 
. Область принятия основной гипотезы на уровне значимости 
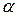определяется неравенствами
Двусторонний критерий: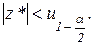 
Правосторонний критерий: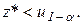 
Левосторонний критерий: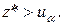 
В противном случае гипотеза 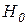отклоняется.
2. Задачи второго типа (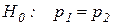) проверяют совпадение параметров двух биномиально распределенных совокупностей. Пусть некоторое событие А в серии из 
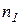испытаний появилось 
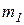раз, а в серии из 
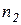испытаний появилось 
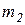раз. Относительная частота появления события А в первой совокупности: 
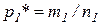. Аналогично 
.
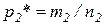Проверяется гипотеза о равенстве появления события А в обеих сериях испытаний 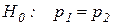. Поскольку вероятности оцениваются по относительным частотам, задачу можно сформулировать так: значимо или незначимо различаются относительные частоты.
Статистика критерия
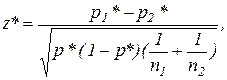
где
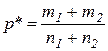- оценка р.
Если верна нулевая гипотеза, то статистика критерия z имеет распределение, близкое к стандартному нормальному закону: z® N(0,1).
Дополнительное условие:
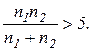
Область принятия основной гипотезы на уровне значимости 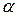определяется неравенствами
Двусторонний критерий: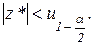
Правосторонний критерий: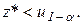
Левосторонний критерий: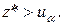
В противном случае гипотеза 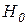отклоняется.
3. Задачи третьего типа (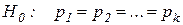) проверяют совпадение параметров биномиально распределенных совокупностей числом больше двух. Пусть некоторое событие А в серии из 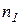испытаний появилось 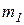раз, в серии из 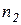испытаний появилось 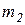раз, …, в серии из 
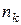испытаний событие А появилось 
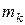раз. Относительная частота появления события А в соответствующих совокупностях: , , …, 
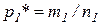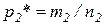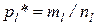
Проверяется гипотеза о равенстве генеральных долей 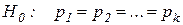. Доказано, что при справедливости нулевой гипотезы и при 
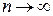статистика критерия
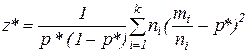
имеет распределение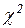 
с k-1 степенями свободы. В В качестве неизвестного значения р* берут наилучшую оценку для p, равную выборочной доле признака, если все k выборок смешать в одну:
.
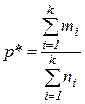Нулевая гипотеза отвергается, если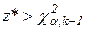 
, где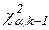 
- критическое значение критерия, определяемое на уровне значимости 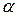при числе степеней свободы k-1.
Гипотезы об ожидаемых числах
Пусть по результатам наблюдений получено некоторое множество значений Ф*i -фактических показателей. При этом вводятся некоторые значения Фi - ожидаемые показатели.
Гипотеза Н0: наблюдаемые показатели совпадают с ожидаемыми (расхождения случайны, связаны с ограниченностью наблюдений).
Доказано, что если Н0 - истина, то статистика критерия
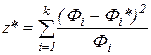
имеет распределение χ2 с числом степеней свободы
ν=(s-1)(r-1),
где s – число строк,
r – число столбцов.
Н0 принимается, если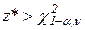 
.
Дополнительное условие: метод применим, если Фi ≥5, иначе нужно объединить данные (k уменьшится).
Используется при проверке гипотез о независимости двух факторов, при проверке гипотезы о функции плотности распределения.
Пример 1. В течение месяца завод поставил предприятию 200 корпусов, из которых 3 оказались дефектными. В следующем месяце было изготовлено 850 корпусов, из которых 7 оказались дефектными. Изменилась ли доля дефектных корпусов в поставках завода? α=0,01
Нулевая гипотеза H0: p1=p2.
Альтернативная H1:p1≠p2
n1= 200 m1=3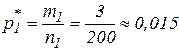 
n2= 850 m1=7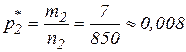 
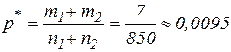
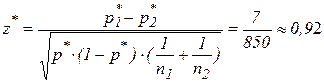
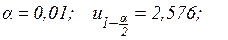
Критерий: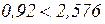 
, основная гипотеза принимается, доли дефектных корпусов за первый и второй месяц не изменились.
Пример 2. В соответствии со стандартом содержание активного вещества в продукции должно составлять 10%. Выборочная контрольная проверка 100 проб показала содержание активного вещества 15%. На уровне значимости α=0,05 выяснить, должна ли продукция быть забракованной?
Нулевая гипотеза H0: p=p0=0,10.
Альтернативная H1: p≠p0=0,10.
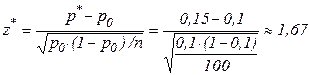
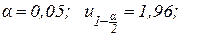
Критерий: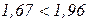 
, основная гипотеза принимается, продукция не должна быть забракованной.
Контрольные вопросы
1. Критерий проверки гипотезы о сравнении параметра биномиального распределения с номиналом.
2. Критерий проверки гипотезы о сопоставлении двух вероятностей биномиальных распределений.
3. Критерий проверки гипотезы о сопоставлении более чем двух вероятностей биномиальных распределений.
