Пропорциональное звено

Это звено называют также усилительным и безынерционным. Звено описывается алгебраическим уравнением y = k × x,

где k – коэффициент передачи (усиления), имеющий размерность единицы выходной величины y, деленную на единицу входной величины x

.

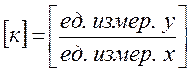Передаточная функция пропорционального звена равна его коэффициенту передачи – W(p) = k.

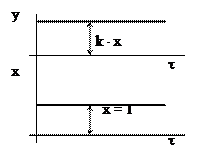Переходная характеристика выглядит следующим образом (рис. 6.1).

Рис. 6.1. Переходная характеристика пропорционального звена

Усилительное звено не трансформирует форму входного сигнала, а изменяет только его масштаб в k раз.

Примерами пропорциональных звеньев могут служить (рис. 6.2):

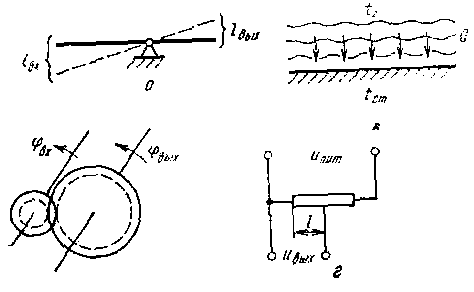Рис. 6.2. Примеры пропорциональных звеньев

а) рычаг, если входная величина х – усилие на одном конце рычага, а выходная величина у – усилие на другом его конце (рис. 6.2,а);

б) зубчатая передача, если х = jвх – угол поворота малой шестерни, а у = jвых – угол поворота большой шестерни (рис. 6.2,б);

в) теплоотдача конвекцией от движущегося газа к стенке, если х –разность температур газа и стенки D t = t_Г – t_СT, а у – количество отдаваемого тепла Q (рис. 6.2,в);

г) потенциометрический датчик измерительного прибора, если х – перемещение движка l, a у – снимаемое с датчика напряжение Uвых (рис. 6.2,г).

6.3.2 Апериодическое (инерционное) звено первого порядка

Динамика этого звена описывается дифференциальным уравнением ,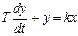

где k – коэффициент передачи; Т – постоянная времени, с.

Передаточная функция звена W(p) = k / (Tp+1).

Переходная характеристика звена h(t) = k (1 – e ^{– t / T}). Таким образом, звено накапливает энергию или вещество и, благодаря этому, Y принимает свое значение через время

Рис. 6.3. Переходная характеристика инерционного звена

На графике переходной функции (рис. 6.3) отрезок, отсекаемый касательной, проведенной в начальной точке, при установившемся значении выходной величины равен постоянной времени Т.

Следовательно, постоянная времени – это время, за которое выходная величина достигла бы своего установившегося значения, если бы изменялась с постоянной начальной скоростью. Чем больше Т, тем длительнее переходный процесс. Практически переходный процесс считается закончившимся через время t» 3 Т.

Примерами апериодических звеньев могут служить:

а) электропривод постоянного тока, если входная величина х подводимое напряжение и, а выходная величина у – скорость вращения n;

б) промежуточный ковш МНЛЗ, если х = Gпр – Gот – баланс поступления и расхода жидкого металла, а у – уровень металла Н;

в) нагрев тела, помещенного в среду с температурой tc (теплоотдача оценивается по закону Ньютона q = a (tc – tм), где q – плотность теплового потока на нагреваемое тело; a – коэффициент теплоотдачи), если tc – входная величина, а средняя температура тела tм – выходная величина;

г) электрическая RC-цепочка, если Uвх = х, а Uвых = у.

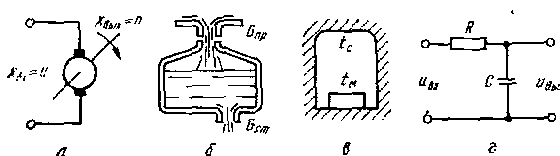Рис. Примеры апериодических звеньев первого порядка

Рис. 6.4. Примеры инерционных звеньев

Астатические (интегрирующие) звенья – это такие звенья, у которых после поступления на вход ступенчатого воздействия выходная величина не приходит к установившемуся значению (как у статических), а непрерывно изменяется.

6.3.3 Идеальное интегрирующее звено

В таком звене выходной сигнал пропорционален интегралу от входной величины. Это свойство звена описывается выражением

или .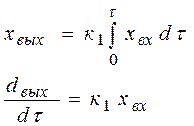

Преобразуем последнее выражение по Лапласу – р у = k₁ х. Тогда передаточная функция звена имеет вид – W(p) = k₁ / p.

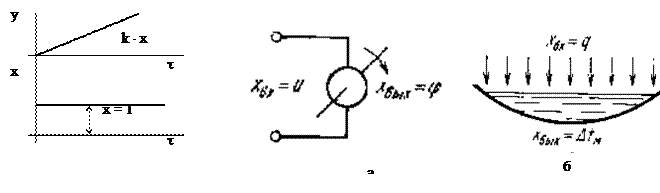
Переходная характеристика звена h(t) = k₁ × t представляет собой прямую линию с углом наклона a = arctg k₁ (рис. 6.5, а).

Примеры интегрирующих звеньев (рис. 6.5, б):

а) электродвигатель, если входная величина – напряжение питания U, а выходная величина – угол поворота якоря j,

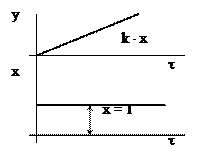б) ванна жидкого металла в сталеплавильной печи, если входная величина – тепловой поток через поверхность ванны q, а выходная величина – изменение средней температуры металла Dt_м.

а б

Рис. 6.5. Интегрирующее звено:

а – переходная характеристика, б – примеры интегрирующих звеньев

6.3.4 Реальное интегрирующее звено (интегрирующее звено с замедлением) описывается дифференциальным уравнением

.

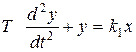Передаточная функция звена W(p) = k₁ / p (Tp + 1).

Переходная характеристика реального интегрирующего звена h(t) = (t - T (1 - e^-t/T)) отличается от переходной функции идеального звена в начальный момент времени, а затем переходит в параллельную ей прямую линию с тем же углом наклона a = arctg k₁ (рис. 6.6).

.

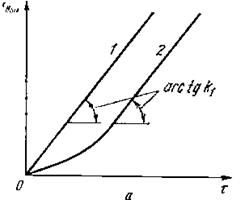Рис. 6.6. Сравнительные переходные характеристики идеального (1) и реального (2) интегрирующих звеньев

Примерами реальных интегрирующих звеньев могут служить те же объекты (см. рис. 6.5), если более точно рассматривать их уравнения движения. Например, электродвигатель с постоянной скоростью вращения будет идеальным интегрирующим звеном. Однако в момент пуска постоянная скорость вала установится не сразу, а с некоторым замедлением и, поэтому, электродвигатель следует рассматривать как реальное интегрирующее звено.

6.3.5 Идеальное дифференцирующее звено

Дифференциальное уравнение звена ,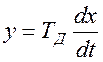

где 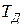– время дифференцирования звена, имеющее размерность единицы выходной величины, деленную на единицу скорости изменения входной величины.

Передаточная функция звена W(p) = Т_Д p.

Переходная характеристика звена h (t) = Т_Д × d (t)

Здесь d (t) – так называемая дельта-функция – мгновенный импульс бесконечно большой амплитуды.. Поєтому переходная характеристика идеального звена представляет собой бросок выходной величины в бесконечность в момент нанесения ступенчатого входного воздействия (рис. 6.7, а).

а б

Рис. 6.7. Пример дифференцирующего звена

Наиболее близко к идеальному звену приближается тахогенератор постоянного тока, если входной величиной считать угол поворота якоря, а выходной – э.д.с. якоря (рис. 6.7, б).

6.3.6 Реальное дифференцирующее звено (дифференцирующее звено с замедлением) описывается дифференциальным уравнением .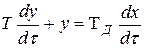

Передаточная функция звена W(p) = Т_Д p / (Tp +1).

Переходная характеристика звена h (t) = (k / T) e ^{– t / T} представляет собой экспоненту, касательная к которой в начальной точке отсекает на нулевом значении выходной величины постоянную времени Т.

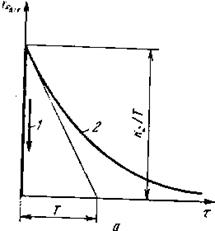
Рис. 6.8. Переходные функции идеального (1) и реального (2)

дифференцирующего звеньев

6.3.7 Звено чистого запаздывания

В отличие от других звеньев, это звено описывается уравнением с запаздывающим аргументом (t – t), где t – время чистого запаздывания у (t) = х (t – t),

Форма сигнала при этом не меняется, он просто смещается во времени.

Передаточная функция этого звена имеет вид – W(p) = k × exp(– p × t), а переходная функция – h(t) = k × (t – t).

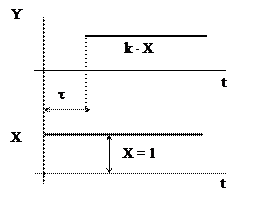Рис. 6.9. Переходная характертистика звена чистого запаздывания

Характерным примером звена чистого запаздывания служит транспортер (например, лента агломерационной машины), на котором после изменения входной величины (толщина слоя сыпучего материала) должно пройти время t₀ = l/v (l – длина транспортера; v – его скорость; t₀ – время чистого транспортного запаздывания), после которого таким же образом изменится выходная величина.

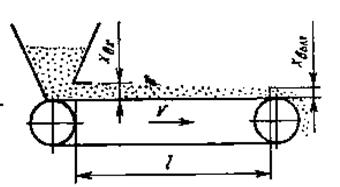Рис. 6.10. Пример звена чистого запаздывания