2015-05-05
352
Если в передаточную функцию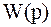 
вместо оператора Лапласа 
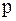подставить мнимую переменную Фурье 
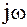, получим частотную передаточную функцию 
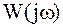, которую называют просто частотной функцией. Ее можно представить в виде действительной 
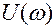и мнимой 
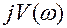частей (компонент)
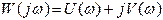
или в комплексной форме
,
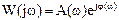где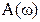 
– модуль частотной функции, а 
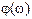– ее фаза.
Покажем связь между компонентами частотной функции и амплитудно–фазовой характеристикой (АФХ). Для этого на комплексной плоскости (рис. 6) отложим действительную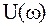 
и мнимую 
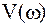части. Если полученную точку А соединить с началом координат, получим вектор 
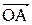, длина (модуль) которого равен 
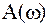, а аргумент (угол, образованный этим вектором с действительной положительной полуосью) 
.
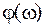Таким образом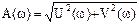 
, 
.
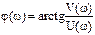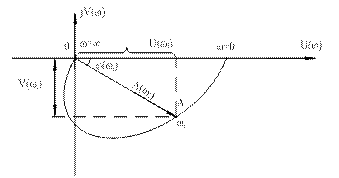
Рис. 6. Построение АФХ по компонентам частотной функции
