За площадь боковой поверхности цилиндра принимается площадь ее развертки

Так как площадь прямоугольника АВВ₁А₁ равна 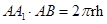, то для вычисления площади S_бок боковой поверхности цилиндра радиуса г и высоты h получается формула: .

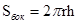Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. Так как площадь каждого основания равна πr², то для вычисления площади полной поверхности цилиндра получаем формулу:

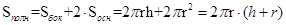
Задача 1. Площадь боковой поверхности цилиндра равна S. Найти: площадь осевого сечения цилиндра (рис.57)

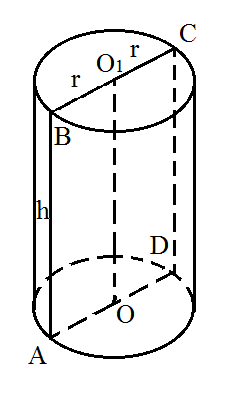
Рис. 57

Решение: 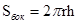. По рисунку (рис. 57) площадь осевого сечения – это площадь прямоугольника ABCD. .

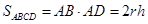Из формулы нахождения площади боковой поверхности: 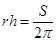. Подставим это выражение в формулу осевого сечения: .

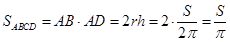Ответ: .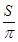

Задача 2. Сколько квадратных метров листовой жести пойдет на изготовление трубы длиной 4 м и диаметром 20 см, если на швы необходимо добавить 2,5% площади ее боковой поверхности?.

Решение. Воспользуемся формулой площади полной поверхности цилиндра: .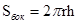

Радиус равен половине диаметра – 0,1м, а высота цилиндра равна длине нужной трубы – 4м.

Так на швы нужно добавить 2,5% площади ее боковой поверхности, нужно найти: (S+2,5%S). Подставим вместо S формулу площади боковой поверхности, и вычислим:

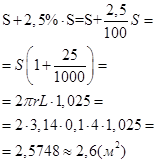
Ответ: 2,6 м².