С помощью интегрирования по частям вычислить неопределённый интеграл от функции вида
1. 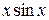 16.
16. 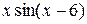
2. 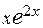 17.
17. 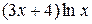
3. 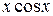 18.
18. 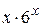
4. 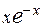 19.
19. 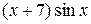
5. 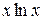 20.
20. 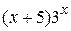
6. 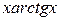 21.
21. 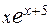
7. 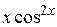 22.
22. 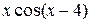
8. 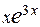 23.
23. 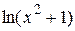
9. 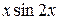 24.
24. 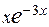
10. 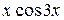 25.
25. 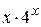
11. 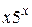 26.
26. 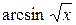
12. 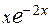 27.
27. 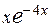
13. 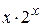 28.
28. 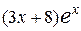
14. 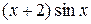 29.
29. 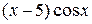
15. 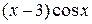 30.
30. 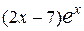
Задача 4.2.
Вычислить неопределённый интеграл с помощью разложения на простейшие дроби подинтегральной функции
1. 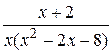 16.
16. 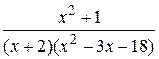
2. 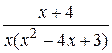 17.
17. 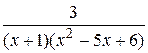
3. 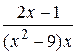 18.
18. 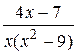
4. 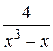 19.
19. 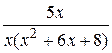
5. 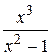 20.
20. 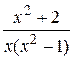
6. 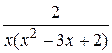 21.
21. 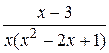
7. 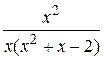 22.
22. 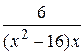
8. 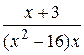 23.
23. 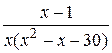
9. 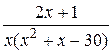 24.
24. 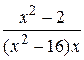
10. 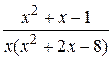 25.
25. 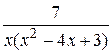
11. 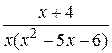 26.
26. 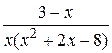
12. 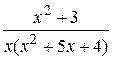 27.
27. 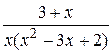
13. 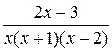 28.
28. 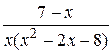
14. 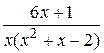 29.
29. 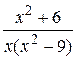
15. 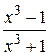 30.
30. 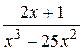
Задача 4.3.
Вычислить с помощью подстановки неопределённый интеграл от функции
1. 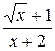 16.
16. 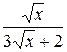
2. 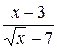 17.
17. 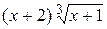
3. 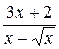 18.
18. 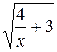
4. 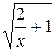 19.
19. 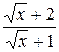
5. 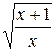 20.
20. 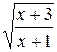
6. 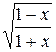 21.
21. 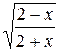
7. 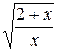 22.
22. 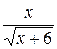
8. 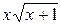 23.
23. 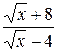
9. 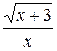 24.
24. 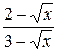
10. 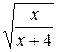 25.
25. 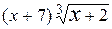
11. 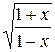 26.
26. 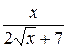
12. 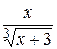 27.
27. 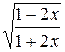
13. 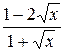 28.
28. 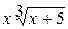
14. 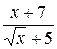 29.
29. 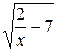
15. 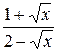 30.
30. 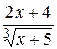
Задача 4.4.
Вычислить с помощью подстановки неопределённый интеграл от функции
1. 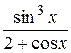 16.
16. 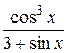
2. 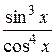 17.
17. 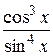
3. 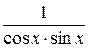 18.
18. 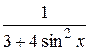
4. 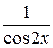 19.
19. 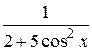
5. 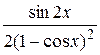 20.
20. 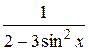
6. 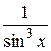 21.
21. 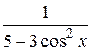
7. 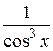 22.
22. 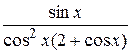
8. 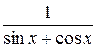 23.
23. 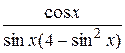
9. 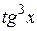 24.
24. 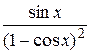
10. 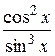 25.
25. 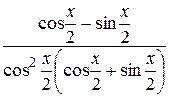
11. 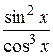 26.
26. 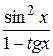
12. 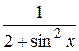 27.
27. 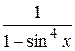
13. 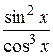 28.
28. 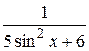
14. 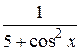 29.
29. 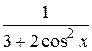
15. 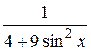 30.
30. 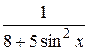
Задача 4.5.
Вычислить площадь фигуры, ограниченной линиями:
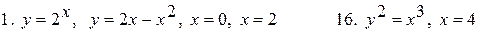














Задача 4.6.
Переходя в полярную систему координат 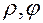 вычислить с помощью опре-деленного интеграла площадь, ограниченную кривыми:
вычислить с помощью опре-деленного интеграла площадь, ограниченную кривыми:
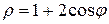
первым витком спирали Архимеда 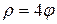 и отрезком полярной оси
и отрезком полярной оси
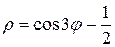
одним лепестком линии 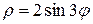
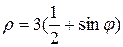
кардиоидой 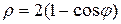 и окружностью
и окружностью 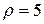
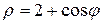
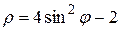
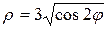
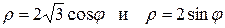
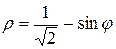
12. одним лепестком линии 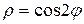
13. четырёхлепестковой розой 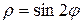
14. лемнискатой Бернулли 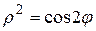
первым и вторым витками спирали Архимеда 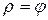 и отрезком полярной
и отрезком полярной
оси
окружностью 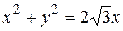 и прямой
и прямой 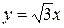
17. 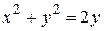 и
и 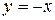 (большая часть)
(большая часть)
18. 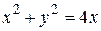 и
и 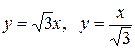
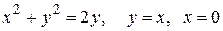
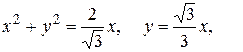 (большая часть)
(большая часть)
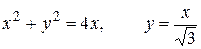
22. 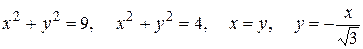 (меньшая часть)
(меньшая часть)
23. 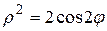 и
и 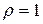
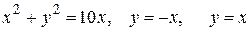
25. 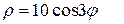 и
и 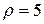
26. 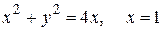 (меньшая часть)
(меньшая часть)
27. 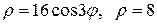 (вне окружности)
(вне окружности)
28. 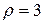 и первого лепестка линии
и первого лепестка линии 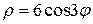
29. 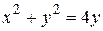 между прямыми
между прямыми 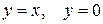
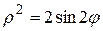
Задача 4.7.
Вычислить несобственный интеграл или доказать его сходимость
1. 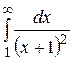 16.
16. 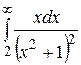
2. 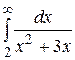 17.
17. 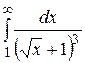
3. 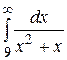 18.
18. 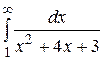
4. 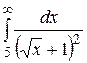 19.
19. 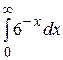
5. 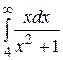 20.
20. 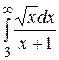
6. 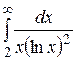 21.
21. 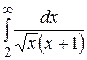
7. 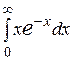
 22.
22. 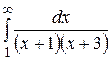
8. 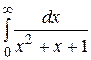 23.
23. 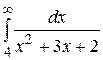
9. 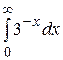 24.
24. 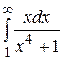
10. 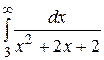 25.
25. 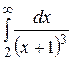
11. 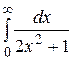 26.
26. 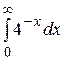
12. 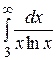 27.
27. 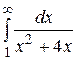
13. 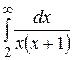 28.
28. 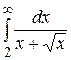
14. 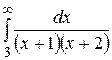 29.
29. 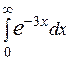
15. 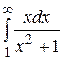 30.
30. 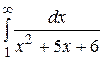
Задача 4.8.
Вычислить массу неоднородной пластины 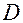 , ограниченной заданными линиями и имеющей поверхностную плотность
, ограниченной заданными линиями и имеющей поверхностную плотность 
| 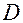
| 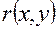
|
| 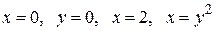
| 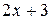
|
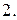
| 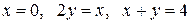
| 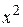
|
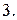
| 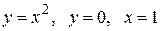
| 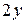
|
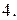
| 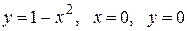
| 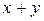
|
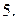
| 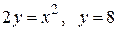
| 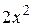
|
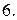
| 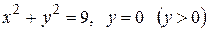
| 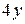
|
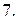
| 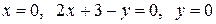
| 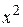
|
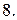
| 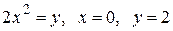
| 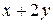
|
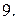
| 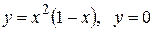
| 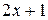
|
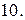
| 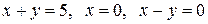
| 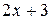
|
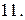
| 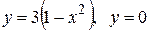
| 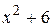
|
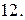
| 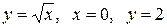
| 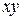
|
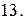
| 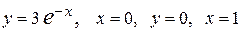
| 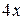
|
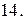
| 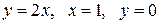
| 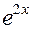
|
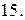
| 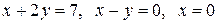
| 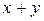
|
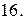
| 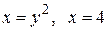
| 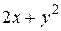
|
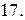
| 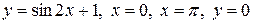
| 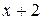
|
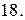
| 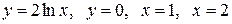
| 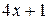
|
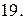
| 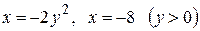
| 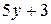
|
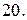
| 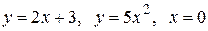
| 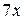
|
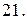
| 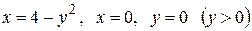
| 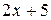
|

| 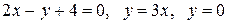
| 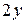
|
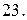
| 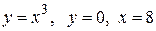
| 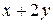
|
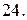
| 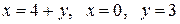
| 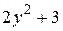
|
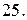
| 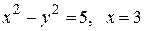
| 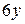
|
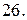
| 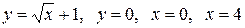
| 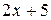
|
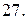
| 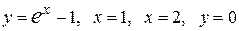
| 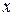
|
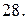
| 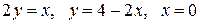
| 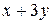
|
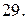
| 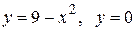
| 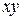
|
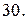
| 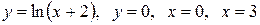
| 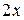
|
Задача 4.9.
Вычислить с помощью тройного интеграла объем области 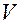 , ограниченной указанными поверхностями.
, ограниченной указанными поверхностями.
| № вар. | 
|
| 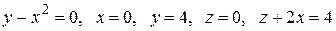
|
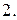
| 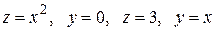
|
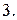
| 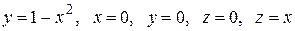
|
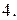
| 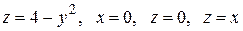
|
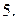
| 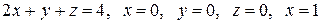
|
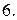
| 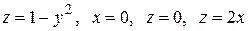
|
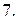
| 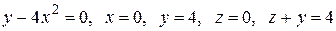
|
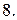
| 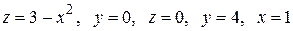
|
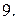
| 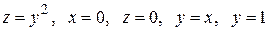
|
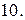
| 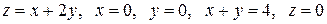
|
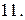
| 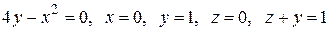
|
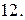
| 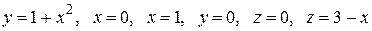
|
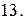
| 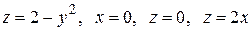
|
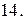
| 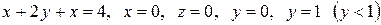
|
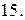
| 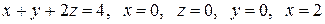
|
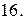
| 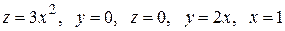
|
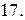
| 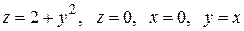
|
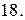
| 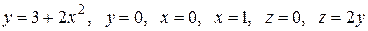
|
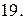
| 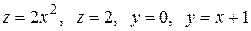
|
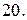
| 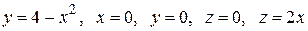
|
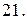
| 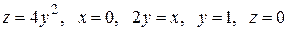
|

| 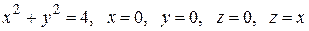
|
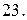
| 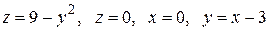
|
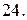
| 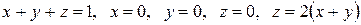
|
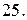
| 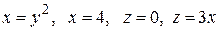
|
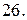
| 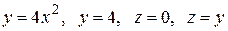
|
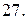
| 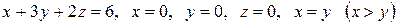
|
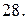
| 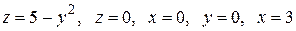
|
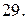
| 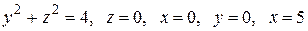
|
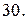
| 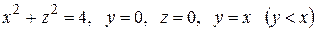
|
Задача 4.10.
Вычислить:
(а) заряд проводника, располагающегося вдоль кривой 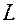 с плотностью
с плотностью 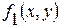 с помощью криволинейного интеграла первого рода
с помощью криволинейного интеграла первого рода 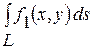
(b) работу силы 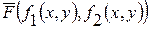 вдоль траектории
вдоль траектории 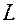 от точки
от точки 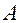 до точки
до точки 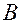 с помощью криволинейного интеграла второго рода
с помощью криволинейного интеграла второго рода 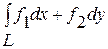
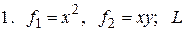 - отрезок прямой между
- отрезок прямой между 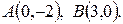
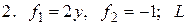 - дуга параболы
- дуга параболы 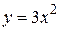 между
между 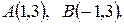
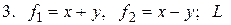 - отрезок прямой между
- отрезок прямой между 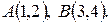
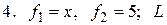 - четверть окружности
- четверть окружности 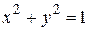 между
между 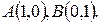
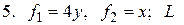 - дуга параболы
- дуга параболы 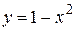 между
между 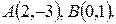
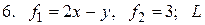 - дуга параболы
- дуга параболы 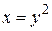 между
между 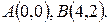
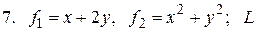 - отрезок прямой между
- отрезок прямой между 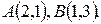
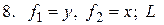 - четверть окружности
- четверть окружности 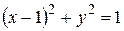 между
между
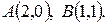
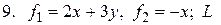 - дуга параболы
- дуга параболы 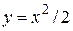 между
между 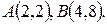
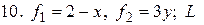 - полуокружность
- полуокружность 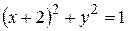 между
между
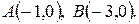
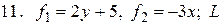 - дуга параболы
- дуга параболы 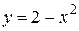 между
между 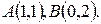
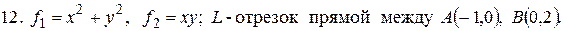
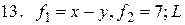 - полуокружность
- полуокружность 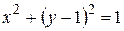 между
между 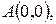
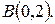
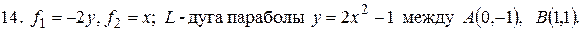
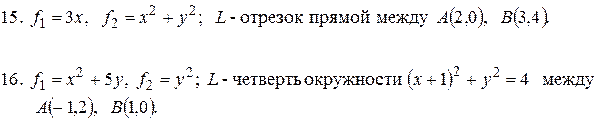
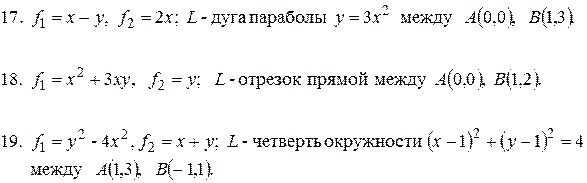
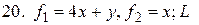 - дуга параболы
- дуга параболы 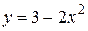 между
между 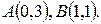
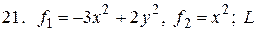 - отрезок прямой между
- отрезок прямой между 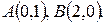
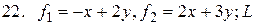 - полуокружность
- полуокружность 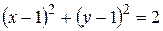
между 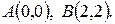
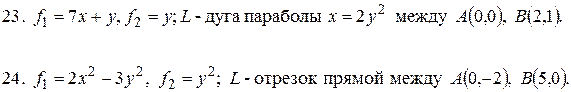
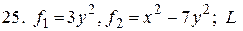 - полуокружность
- полуокружность 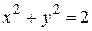 между
между
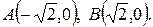

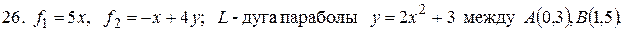
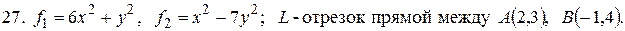
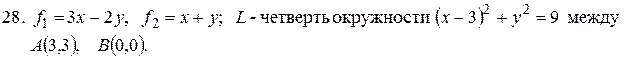
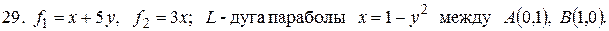
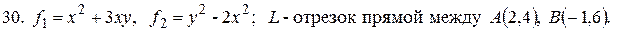
Задача 4.11.
С помощью поверхностного интеграла первого рода
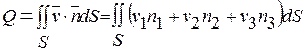

вычислить расход 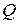 жидкости с полем скоростей
жидкости с полем скоростей
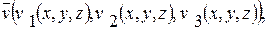 протекающей за единицу времени через часть
протекающей за единицу времени через часть 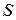 плоскости
плоскости 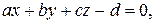 лежащую в первом октанте. Единичная нормаль
лежащую в первом октанте. Единичная нормаль 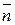 направлена вне начала координат.
направлена вне начала координат.
| № вар. | 
| 
| 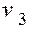
| 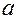
| 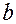
| 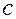
| 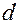
|
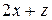
| 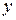
| ||||||
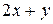
| 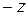
| ||||||
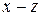
| 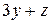
| ||||||
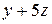
| 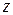
| 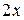
| |||||
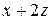
| 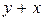
| ||||||
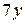
| 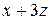
| ||||||
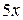
| 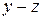
| ||||||
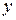
| 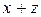
| 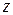
| |||||
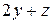
| 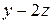
| ||||||
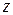
| 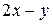
| 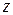
| |||||
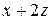
| 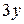
| ||||||
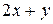
| 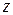
| ||||||
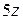
| 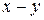
| ||||||
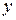
| 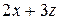
| ||||||
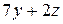
| 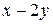
| ||||||
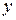
| 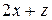
| ||||||
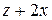
| 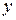
| ||||||
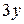
| 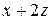
| ||||||
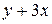
| 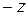
| ||||||
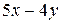
| 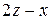
| ||||||
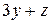
| 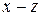
| ||||||
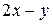
| 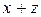
| ||||||
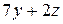
| 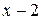
| ||||||
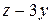
| 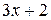
| ||||||
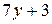
| 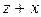
| -8 | |||||
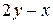
| 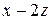
| 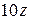
| |||||
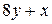
| 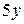
| 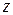
| |||||
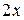
| 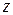
| 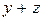
| |||||
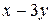
| 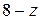
| ||||||
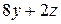
| 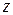
|
4. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КОНТРОЛЬНЫХ РАБОТ
4.1. Решение типового варианта контрольной работы №1
Задача 1.1. Дана система линейных неоднородных алгебраических уравнений
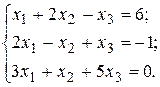
Совместность данной системы проверим по теореме Кронекера-Капелли. С помощью элементарных преобразований расширенную матрицу 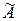 приведем к трапециевидной форме
приведем к трапециевидной форме
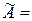
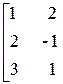
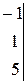
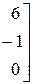 ~
~ 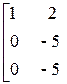
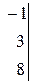
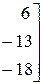 ~
~ 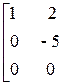
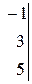
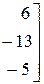 .
.
Следовательно, 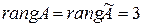 (числу неизвестных системы). Значит, исходная система совместна и имеет единственное решение.
(числу неизвестных системы). Значит, исходная система совместна и имеет единственное решение.
а). По формулам Крамера: 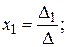
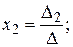
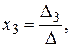 где
где
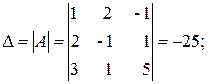
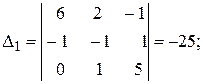
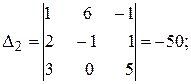
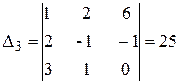 .
.
Находим 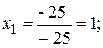
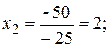
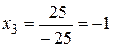 .
.
б). С помощью обратной матрицы 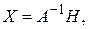 где
где 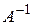 - обратная матрица к
- обратная матрица к 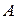 ,
, 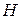 - столбец правых частей.
- столбец правых частей.
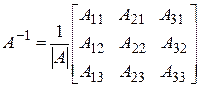 .
.
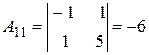 ;
; 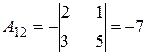 ;
; 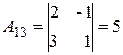 ;
;
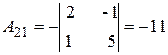 ;
; 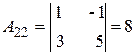 ;
; 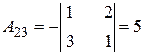 ;
;
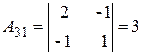 ;
; 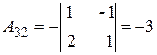 ;
; 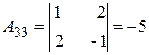 .
.
Решение системы
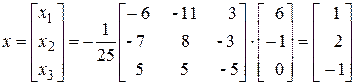 ,
,
т.е. 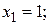
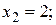
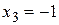 .
.
в). Наша система эквивалентна
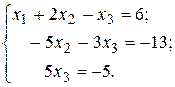
(прямой ход Гаусса совершен при нахождении рангов матриц 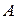 и
и 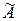 ).
).
Тогда 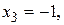
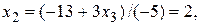
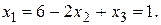
Задача 1.2. Решить однородную систему линейных алгебраических уравнений
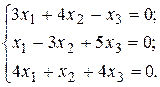
С помощью элементарных преобразований матрицу 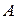 приведем к трапециевидной форме
приведем к трапециевидной форме
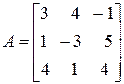 ~
~ 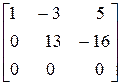 .
.
Следовательно, 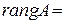 2<3 и система имеет бесконечное множество решений, зависящих от 3-2=1 произвольной постоянной. Исходная система эквивалентна
2<3 и система имеет бесконечное множество решений, зависящих от 3-2=1 произвольной постоянной. Исходная система эквивалентна
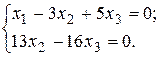
Откуда 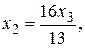
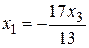 .
.
Полагая 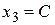 (произвольной постоянной), имеем
(произвольной постоянной), имеем
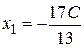 ,
, 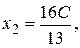
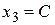 .
.
Задача 1.3. По координатам точек 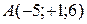 ,
, 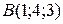 ,
, 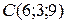 найти:
найти:
а). Модуль вектора 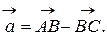
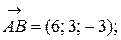
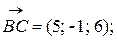
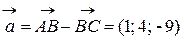 ;
;
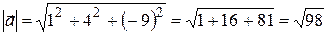 .
.
б). Скалярное произведение векторов 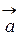 и
и 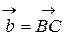 .
.
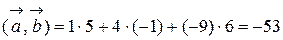 .
.
в). Проекцию вектора  на вектор
на вектор  .
.
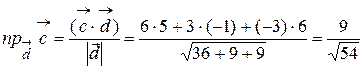 .
.
г). Координаты точки 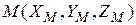 , делящей отрезок
, делящей отрезок 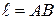 в отношении 1:3;
в отношении 1:3; 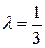 . Следовательно:
. Следовательно:
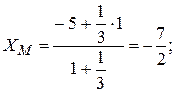
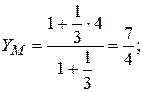
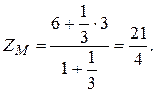
Задача 1.4. Даны векторы 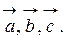 Необходимо:
Необходимо:
а). Найти модуль векторного произведения 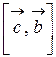 .
.
 =
=
 2015-05-05
2015-05-05 444
444








